题目内容
10.把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.如:①用配方法分解因式:a2+6a+8,
解:原式=a2+6a+8+1-1=a2+6a+9-1=(a+2)(a-4)
②M=a2-2ab+2b2-2b+2,利用配方法求M的最小值,
解:a2-2ab+2b2-2b+2=a2-2ab+b2+b2-2b+1+1=(a-b)2+(b-1)2+1
∵(a-b)2≥0,(b-1)2≥0
∴当a=b=1时,M有最小值1.
请根据上述材料解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:x2-$\frac{2}{3}$x+$\frac{1}{9}$.
(2)用配方法因式分解:x2-4xy+3y2.
(3)若M=$\frac{1}{4}$x2+2x-1,求M的最小值.
(4)已知x2+2y2+z2-2xy-2y-4z+5=0,则x+y+z的值为4.
分析 (1)加一次项系数一半的平方,配成完全平方式;
(2)将3y2化成4y2-y2,前三项配成完全平方式,再利用平方差公式进行因式分解;
(3)提取系数$\frac{1}{4}$后,再加一次项系数一半的平方16,并减去16,配成完全平方式,利用平方≥0可知M的最小值;
(4)拆项后配成三个完全平方式,利用平方≥0可知:要想使已知式成立则存在$\left\{\begin{array}{l}{x-y=0}\\{y-1=0}\\{z-2=0}\end{array}\right.$,求出x、y、z的值并相加即可.
解答 解:(1)x2-$\frac{2}{3}$x+$\frac{1}{9}$=$(x-\frac{1}{3})^{2}$,
故答案为:$\frac{1}{9}$;
(2)x2-4xy+3y2=x2-4xy+4y2-y2=(x-2y)2-y2=(x-2y+y)(x-2y-y)=(x-y)(x-3y);
(3)M=$\frac{1}{4}$x2+2x-1,
M=$\frac{1}{4}$(x2+8x+16-16)-1=$\frac{1}{4}$(x+4)2-5,
∵$\frac{1}{4}$(x+4)2≥0,
∴当x=-4时,M有最小值为-5;
(4)x2+2y2+z2-2xy-2y-4z+5=0,
x2-2xy+y2+y2-2y+1+z2-4z+4=0,
(x-y)2+(y-1)2+(z-2)2=0,
∵x-y≥0,y-1≥0,z-2≥0,
∴$\left\{\begin{array}{l}{x-y=0}\\{y-1=0}\\{z-2=0}\end{array}\right.$,
∴x=1,y=1,z=2,
∴x+y+z=1+1+2=4,
故答案为:4.
点评 本题考查了利用配方法解决数学中的问题;把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法;配方法在数学中应用比较广泛,既可以利用配方法进行因式分解,也可以利用配方法求最小值,同时对于(4)中几个非负数的和为零时,可得这几个加数同时为零,求出未知数的值,这一知识在数学中经常运用,要熟练掌握.

| A. | m$>\frac{1}{3}$ | B. | m$<\frac{1}{3}$ | C. | m$≥\frac{1}{3}$ | D. | m$≤\frac{1}{3}$ |
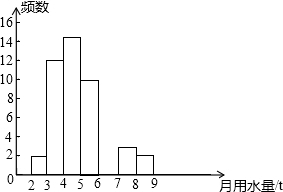 小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 15 | 30% |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.
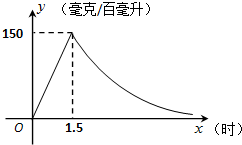 实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:
实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题: 如图,已知点B,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点A,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的同侧,AB=4,CD=3,AB与CD的距离为1,则a-b的值是12.
如图,已知点B,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点A,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的同侧,AB=4,CD=3,AB与CD的距离为1,则a-b的值是12.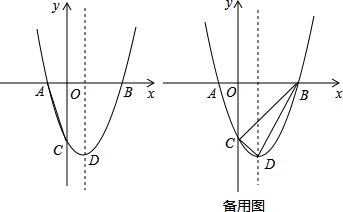
 已知关于x的二次函数y=x2+(2k-1)x+k2-1,且关于x的方程x2+(2k-1)x+k2-1=0的两根的平方和等于9.
已知关于x的二次函数y=x2+(2k-1)x+k2-1,且关于x的方程x2+(2k-1)x+k2-1=0的两根的平方和等于9. 如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是3$\sqrt{3}$.
如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是3$\sqrt{3}$.