题目内容
19、如图，AB与AC是⊙O的两条等弦，过C作⊙O的切线与BA的延长线相交于点D，DE垂直于AC交CA延长线于E，则AE：AD=（ ）分析：由勾股定理得，BD•DA=DC2，即BD•（BD-BA）=（AC+AE）2+（BD-AB）2-AE2，从而得出AE：AD=1：2．
解答：解：由切割线定理，得BD•DA=DC2，
∴BD•（BD-BA）=CE2+ED2=（AC+AE）2+（BD-AB）2-AE2，
∴AC+2AE=BD，
∴2AE=AD，
∴AE：AD=1：2．
故选D．
∴BD•（BD-BA）=CE2+ED2=（AC+AE）2+（BD-AB）2-AE2，
∴AC+2AE=BD，
∴2AE=AD，
∴AE：AD=1：2．
故选D．
点评：本题考查了切割线定理和勾股定理，是基础知识要熟练掌握．
练习册系列答案
相关题目
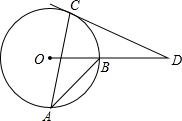如图，AB、AC是⊙O的两条弦∠A=25°，过点C的切线与OB的延长线交于点D，则∠D的度数是
如图，AB、AC是⊙O的弦，AD⊥BC于点D，交⊙O于点F，AE是⊙O的直径，试判断弦BE与弦CF的大小关系，并说明理由．
如图，AB与AC是⊙O的两条等弦，过C作⊙O的切线与BA的延长线相交于点D，DE垂直于AC交CA延长线于E，则AE：AD=