Question

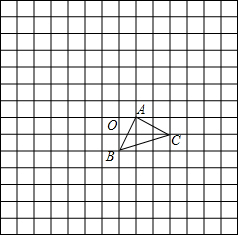
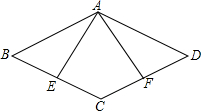
（1）如图，在菱形ABCD中，点E是AB上的一点，连接DE交AC于点O，连接BO，且∠AED=50°，则∠CBO________度．

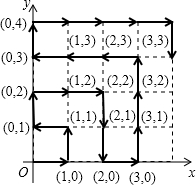
（2）在平面直角坐标系中，有若干个整数点，其顺序按图中“?”方向排列，如（0，0），（1，0），（1，1），（0，1），（0，2），（1，2），（2，2），（2，1），（2，0）（3，0）…
按此规律，第95个点的坐标是________．

Answer 1

解：（1）
∵在菱形ABCD中，
∴AB=AD，∠DAO=∠BAO，
∴，
∴△AOB≌△AOD（SAS），
∴∠ADO=∠ABO，
在△AED中，∠AED+∠BAD+∠ADB=180°，
由AD∥BC可得∠OBC+∠ABO+∠BAD=180°
∴∠CBO=∠AED=50°

（2）第一个正方形上有4个点，添上第二个正方形后，一共有3×3=9个点，添上第三个正方形后，一共有4×4=16个点
∵添上第8个正方形后，一共有9×9=81个点
∴第95个点应在第9个正方形上，第9个正方形最后的那个数的坐标为（0，9），减去5个数即是第95个数，然后依次向右转为（9，4）．
故答案为（9，4）．
分析：（1）利用SAS判定△AOB≌△AOD从而得到对应角相等，再根据平行线的性质即可求得∠CBO的度数；
（2）根据已知可推出第95个点应在第9个正方形上，可坟得第9个正方形最后一个数的坐标，依次向右转5个数即可求得其坐标．
点评：需注意利用菱形的性质来求得相应的角相等；解决有规律题的关键是通过横向，纵向观察得到相应的规律．