题目内容
 已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.
已知:如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC.(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;
(2)线段DM与AM有怎样的位置关系?请说明理由.
分析:(1)过点M作ME⊥AD,垂足为E,先求出ME=MC,再求出ME=MB,从而证明AM平分∠DAB;
(2)利用两直线平行同旁内角互补可得∠1+∠3=90°,所以两直线垂直.
(2)利用两直线平行同旁内角互补可得∠1+∠3=90°,所以两直线垂直.
解答:解:(1)AM平分∠DAB,理由为:
证明:过点M作ME⊥AD,垂足为E,
∵DM平分∠ADC ,
,
∴∠1=∠2,
∵MC⊥CD,ME⊥AD,
∴ME=MC(角平分线上的点到角两边的距离相等),
又∵MC=MB,∴ME=MB,
∵MB⊥AB,ME⊥AD,
∴AM平分∠DAB(到角的两边距离相等的点在这个角的平分线上).
(2)AM⊥DM,理由如下:
∵∠B=∠C=90°,
∴DC⊥CB,AB⊥CB,
∴CD∥AB(垂直于同一条直线的两条直线平行),
∴∠CDA+∠DAB=180°(两直线平行,同旁内角互补)
又∵∠1=
∠CDA,∠3=
∠DAB(角平分线定义)
∴2∠1+2∠3=180°,∴∠1+∠3=90°,
∴∠AMD=90度.即AM⊥DM.
证明:过点M作ME⊥AD,垂足为E,
∵DM平分∠ADC
 ,
,∴∠1=∠2,
∵MC⊥CD,ME⊥AD,
∴ME=MC(角平分线上的点到角两边的距离相等),
又∵MC=MB,∴ME=MB,
∵MB⊥AB,ME⊥AD,
∴AM平分∠DAB(到角的两边距离相等的点在这个角的平分线上).
(2)AM⊥DM,理由如下:
∵∠B=∠C=90°,
∴DC⊥CB,AB⊥CB,
∴CD∥AB(垂直于同一条直线的两条直线平行),
∴∠CDA+∠DAB=180°(两直线平行,同旁内角互补)
又∵∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴2∠1+2∠3=180°,∴∠1+∠3=90°,
∴∠AMD=90度.即AM⊥DM.
点评:本题主要考查了垂直平分线上的点到线段两端的距离相等的性质和它的逆定理,及平行线的性质.正确作出辅助线是解答本题的关键.

练习册系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为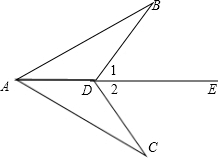 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为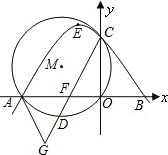 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧