题目内容
11.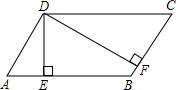 如图,在平行四边形ABCD中,DE⊥AB交AB于点E,DF⊥BC交BC于点F,若∠EDF=60°,DE=4$\sqrt{3}$,DF=5$\sqrt{3}$,求平行四边形ABCD的面积.
如图,在平行四边形ABCD中,DE⊥AB交AB于点E,DF⊥BC交BC于点F,若∠EDF=60°,DE=4$\sqrt{3}$,DF=5$\sqrt{3}$,求平行四边形ABCD的面积.
分析 根据四边形内角和定理得出∠EBF=120°,再利用平行四边形的性质以及锐角三角函数关系得出AD的长,即可得出答案.
解答 解:∵DE⊥AB,DF⊥BC,∠EDF=60°,
∴∠EBF=120°,
∴∠A=∠C=60°,
∵DE=4$\sqrt{3}$,
∴sin60°=$\frac{DE}{AD}$=$\frac{4\sqrt{3}}{AD}$=$\frac{\sqrt{3}}{2}$,
解得:AD=8,则BC=8,
故平行四边形ABCD的面积为:BC×DF=8×5$\sqrt{3}$=40$\sqrt{3}$.
点评 此题主要考查了平行四边形的性质以及锐角三角函数关系,得出AD的长是解题关键.

练习册系列答案
相关题目
1.一个多边形的各个内角都等于120°,则它的边数为( )
| A. | 3 | B. | 6 | C. | 7 | D. | 8 |
19.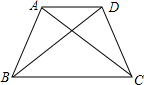 如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
 如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )| A. | $4\sqrt{2}$ | B. | 4 | C. | $2\sqrt{2}$ | D. | 2 |
3.某篮球队12名队员的年龄如表:
则这12名队员年龄的众数和中位数分别是18、19.
| 年龄(岁) | 18 | 19 | 20 | 21 |
| 人数 | 5 | 4 | 1 | 2 |
1.下列几何体的主视图与其他主视图不一样的是( )
| A. |  | B. |  | C. |  | D. |  |
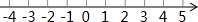 不等式组$\left\{\begin{array}{l}{3x>x-2}\\{\frac{x+1}{3}>2x}\end{array}\right.$,并把解集在数轴上正确表示出来.
不等式组$\left\{\begin{array}{l}{3x>x-2}\\{\frac{x+1}{3}>2x}\end{array}\right.$,并把解集在数轴上正确表示出来.