题目内容
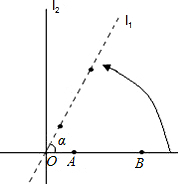如图所示，直线l1⊥l2，垂足为点O，A、B是直线l1上的两点，且OB=2，AB=| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
分析：如图，以点B为圆心，AB为半径画圆，与l2的交点即是P点．则在直角三角形OBD中，解直角三角形，即可求解．
解答：
解：（1）在直线l2上找点P，使得△BPA是以∠B为顶角的等腰三角形，
则以点B为圆心，AB为半径画圆即可．
与l2的交点就是点P．
从B点作OP的高BD，
则在直角三角形OBD中，解直角三角形可知：OD=
，
所以PO=
-1或
+1．
故答案为：
-1或
+1．
解：（1）在直线l2上找点P，使得△BPA是以∠B为顶角的等腰三角形，则以点B为圆心，AB为半径画圆即可．
与l2的交点就是点P．
从B点作OP的高BD，
则在直角三角形OBD中，解直角三角形可知：OD=
| 3 |
所以PO=
| 3 |
| 3 |
故答案为：
| 3 |
| 3 |
点评：本题综合考查了旋转与等腰三角形的知识，注意要做等腰三角形，腰一端的为顶点画圆是最好的方法．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
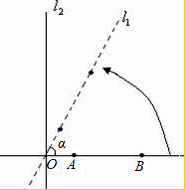如图所示，直线L1⊥L2，垂足为点O，A，B是直线L1上的两点，且OB=2，AB=
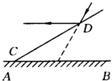44、如图所示，直线L1∥L2，C1，C2，C3是L1上的三点，连接C1A，C1B，C2A，C2B，C3A，C3B，得△C1AB，△C2AB，△C3AB，试说明△C1AB，△C2AB，△C3AB的面积相等．
2、如图所示，直线l1∥l2，∠1=40°，则∠2为（ ）