题目内容
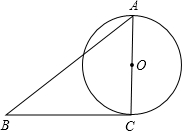如图已知△ABC的一边BC与以AC为直径的⊙O相切于点C，若BC=4，AB=5，则sinB=分析：根据BC与以AC为直径的⊙O相切于点C，即可证得△ABC是直角三角形，然后根据勾股定理即可求得AC的长，根据正弦函数的定义即可求解．
解答：解：∵BC是⊙O的切线，
∴∠ACB=90°，
∴在直角△ABC中，AC=
=
=3，
∴sinB=
=
．
故答案是：
．
∴∠ACB=90°，
∴在直角△ABC中，AC=
| AB2-BC2 |
| 52-42 |
∴sinB=
| AC |
| AB |
| 3 |
| 5 |
故答案是：
| 3 |
| 5 |
点评：本题主要考查了正弦函数的定义，勾股定理以及切线的性质定理，根据切线这一条件，证得△ABC是直角三角形是关键．
练习册系列答案
科学实验活动册系列答案
相关题目
（2013•嘉定区一模）如图已知△ABC中AB=AC=10，BC=16，矩形DEFG的边EF在△ABC的边BC上，顶点D、G分别在AB、AC上，设DE的长为x，矩形DEFG的面积为y，求y关于x的函数关系式，并写出这个函数的定义域．
