题目内容
如图,已知△ABC是一等腰三角形铁板余料,其中AB=AC=20cm,BC=24cm.若在△ABC上截出一矩形零件DEFG,使EF在BC上,点D、G分别在边AB、AC上.问矩形DEFG的最大面积是多少?
【答案】
96cm2
【解析】
试题分析:过A作AM⊥BC于M,交DG于N, 设DE=xcm,S矩形=ycm2,证得△ADG∽△ABC,根据相似三角形的性质即可表示出DG,再根据矩形的面积公式得到y关于x的函数关系式,最后根据二次函数的性质即可求得结果.
过A作AM⊥BC于M,交DG于N,

则AM= =16cm.
=16cm.
设DE=xcm,S矩形=ycm2,则由△ADG∽△ABC,
故 ,即
,即 ,故DG=
,故DG= (16-x).
(16-x).
∴y=DG·DE= (16-x)x=-
(16-x)x=- (x2-16x)=-
(x2-16x)=- (x-8)2+96,
(x-8)2+96,
从而当x=8时,y有最大值96.即矩形DEFG的最大面积是96cm2.
考点:二次函数的应用
点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 的坐标为(-1,0).
的坐标为(-1,0). 如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.
如图,已知△ABC是等边三角形,AB交⊙O于点D,DE⊥AC于点E.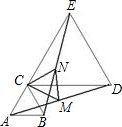 如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,
如图,已知△ABC是等边三角形,E是AC延长线上一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点, (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF. (2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.
(2013•奉贤区二模)如图,已知△ABC是等边三角形,点D是BC延长线上的一个动点,以AD为边作等边△ADE,过点E作BC的平行线,分别交AB,AC的延长线于点F,G,联结BE.