Question

【题目】如图，在矩形OABC中，OA＝3，OC＝4，分别以OA、OC所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y＝（k＞0）的图象经过点D且与边BA交于点E，作直线DE．

（1）当点D运动到BC中点时，求k的值；

（2）求的值；

（3）连接DA，当△DAE的面积为时，求k值．

Answer 1

【答案】（1）k＝6；（2）；（3）当△DAE的面积为时，k的值为4或8．

【解析】

（1）由OA，OC的长度结合矩形的性质可得出BC的长度及点B的坐标，根据点D为边BC的中点可得出CD的长度，进而可得出点D的坐标，再利用反比例函数图象上点的坐标特征即可求出k值；

（2）由OA，OC的长度利用反比例函数图象上点的坐标特征可求出点D，E的坐标，进而可得出BD，BE的长度，二者相比后即可得出的值；

（3）由（2）可得出AE，BD的长度，由三角形的面积公式结合S△DAE＝即可得出关于k的一元二次方程，解之即可得出k值．

（1）∵OA＝3，OC＝4，四边形OABC为矩形，

∴BC＝OA＝3，点B的坐标为（3，4）．

∵点D为边BC的中点，

∴CD＝BC＝，

∴点D的坐标为（，4）．

又∵点D在反比例函数y＝（k＞0）的图象上，

∴k＝×4＝6．

（2）∵点D，E在反比例函数y＝（k＞0）的图象上，

∴点D的坐标为（，4），点E的坐标为（3，）．

又∵点B的坐标为（3，4），

∴BD＝3﹣，BE＝4﹣，

∴．

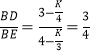（3）由（2）可知：AE＝，BD＝3﹣，

∴S△DAE＝AEBD＝××（3﹣）＝，

整理，得：k2﹣12k+32＝0，

解得：k1＝4，k2＝8，

∴当△DAE的面积为时，k的值为4或8．