题目内容
【题目】如图,直线y=k1x+b(k1≠0)与双曲线![]() (k2≠0)相交于A(1,2)、B(m,﹣1)两点.
(k2≠0)相交于A(1,2)、B(m,﹣1)两点.
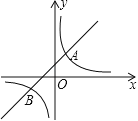
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<0<x2<x3,请直接写出y1,y2,y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b<![]() 的解集.
的解集.
【答案】(1) y=x+1
(2)y2>y3>y1
(3) ﹣2<x<0或x>1
【解析】
(1)将A坐标代入反比例解析式中求出k2的值,确定出双曲线解析式,将B坐标代入反比例解析式求出m的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出k1与b的值,即可确定出直线解析式。
(2)根据三点横坐标的正负,得到A2与A3位于第一象限,对应函数值大于0,A1位于第三象限,函数值小于0,且在第一象限为减函数,即可得到大小关系式:
∵x1<0<x2<x3,且反比例函数在第一象限为减函数,
∴A2与A3位于第一象限,即y2>y3>0,A1位于第三象限,即y1<0,
则y2>y3>y1。
(3)由两函数交点坐标,利用图象即可得出所求不等式的解集。
解:(1)将A(1,2)代入双曲线解析式得:k2=2,即双曲线解析式为![]() 。
。
将B(m,﹣1)代入双曲线解析式得:![]() ,即m=﹣2,∴B(﹣2,﹣1)。
,即m=﹣2,∴B(﹣2,﹣1)。
将A与B坐标代入直线解析式得:![]() ,解得:
,解得:![]() 。
。
∴直线解析式为y=x+1。
(2)y2>y3>y1。
(3)由A(1,2),B(﹣2,﹣1),
利用函数图象得:不等式k1x+b<![]() 的解集为﹣2<x<0或x>1。
的解集为﹣2<x<0或x>1。

 优百分课时互动系列答案
优百分课时互动系列答案【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(度) | 电费价格(元/度) |
| 0.48 |
| 0.53 |
| 0.78 |
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,则李叔家七月份最多可用电的度数是( ).
A. 100B. 400C. 396D. 397