题目内容
6. 如图,△ABD,△AEC都是等边三角形.若CD与BE相交于点O.求证:
如图,△ABD,△AEC都是等边三角形.若CD与BE相交于点O.求证:(1)BE=DC;
(2)∠BOD=60°.
分析 (1)由条件可证明△ADC≌△ABE,可证得BE=DC;
(2)由(1)可得出∠ADC=∠ABE,根据三角形的内角和定理求出∠BOD=180°-∠ODB-∠DBA-∠ABE=60°,
解答 证明:
(1)∵△ABD与△AEC都是等边三角形,
∴AD=AB,AE=AC,∠ADB=∠ABD=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$
∴△DAC≌△BAE(SAS),
∴BE=DC;
(2)由(1)可得出∠ADC=∠ABE,
∵∠BOD=180°-∠ODB-∠DBA-∠ABE
=180°-∠ODB-60°-∠ADC
=120°-(∠ODB+∠ADC)
=120°-60°=60°,
∴∠BOD=60°.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
1.下列图形具有稳定性的是( )
| A. | 正方形 | B. | 长方形 | C. | 钝角三角形 | D. | 平行四边形 |
11.下列计算正确的是( )
| A. | (x+y)2=x2+y2 | B. | (x-y)2=x2-2xy-y2 | C. | (x+2y)(x-2y)=x2-2y2 | D. | (x-y)2=x2-2xy+y2 |
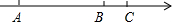 已知如图数轴上A、B、C三点,AB=2BC,A、B表示的数分别是-2$\sqrt{2}$和1,则C表示的数为$\frac{3}{2}$+$\sqrt{2}$.
已知如图数轴上A、B、C三点,AB=2BC,A、B表示的数分别是-2$\sqrt{2}$和1,则C表示的数为$\frac{3}{2}$+$\sqrt{2}$.