题目内容
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且当
,且当![]() 和
和![]() 时二次函数的函数值
时二次函数的函数值![]() 相等.
相等.
(![]() )求实数
)求实数![]() 、
、![]() 的值.
的值.
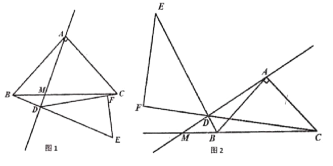
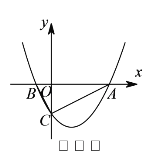
(![]() )如图
)如图![]() ,动点
,动点![]() 、
、![]() 同时从
同时从![]() 点出发,其中点
点出发,其中点![]() 以每秒
以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 边向终点
边向终点![]() 运动,点
运动,点![]() 以每秒
以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向运动,当点
方向运动,当点![]() 停止运动时,点
停止运动时,点![]() 随之停止运动.设运动时间为
随之停止运动.设运动时间为![]() 秒.连接
秒.连接![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在点
落在点![]() 处,得到
处,得到![]() .
.
①是否存在某一时刻![]() ,使得
,使得![]() 为直角三角形?若存在,求出
为直角三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
②设![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
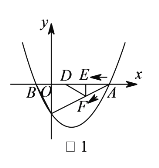
【答案】(1)![]() ,
,![]() ;(2)①存在,
;(2)①存在,![]() 或
或![]() ;②当
;②当![]() 时,
时, ![]() ;当
;当![]() 时,S
时,S![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)根据抛物线图象经过点A以及“当x=-2和x=5时二次函数的函数值y相等”两个条件,列出方程组求出待定系数的值.
(2)①首先由抛物线解析式能得到点A、B、C三点的坐标,则线段OA、OB、OC的长可求,进一步能得出AB、BC、AC的长;首先用t 表示出线段AD、AE、AF(即DF)的长,则根据AE、EF、OA、OC的长以及公共角∠OAC能判定△AEF、△AOC相似,那么△AEF也是一个直角三角形,及∠AEF是直角;若△DCF是直角,可分成三种情况讨论:
1、点C为直角顶点,由于△ABC恰好是直角三角形,且以点C为直角顶点,所以此时点B、D重合,由此得到AD的长,进而求出t的值;
2、点D为直角顶点,此时∠CDB与∠CBD恰好是等角的余角,由此可证得OB=OD,再得到AD的长后可求出t的值;
3、点F为直角顶点,当点F在线段AC上时,∠DFC是锐角,而点F在射线AC的延长线上时,∠DFC又是钝角,所以这种情况不符合题意.
②此题需要分三种情况讨论:
1、当点E在点A与线段AB中点之间时,两个三角形的重叠部分是整个△DEF;
2、当点E在线段AB中点与点O之间时,重叠部分是个不规则四边形,那么其面积可由大直角三角形与小钝角三角形的面积差求得;
3、当点E在线段OB上时,重叠部分是个小直角三角形.
(![]() )由题意得:
)由题意得:![]() ,解得:
,解得:![]() ,
,![]() .
.
(![]() )①由(
)①由(![]() )知
)知![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 为
为![]() ,且
,且![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴翻折后,![]() 落在
落在![]() 处,∴
处,∴![]() ,
,
∴![]() ,
,![]() ,
,
若![]() 为
为![]() ,点
,点![]() 在
在![]() 上时,
上时,
i)∴若![]() 为直角顶点,则
为直角顶点,则![]() 与
与![]() 重合,
重合,
∴![]() ,
,![]() ,如图
,如图![]()
ii)若![]() 为直角顶点,∵
为直角顶点,∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,如图
,如图![]()
当点![]() 在
在![]() 延长线上时,
延长线上时,![]() ,
,![]() 为钝角三角形,
为钝角三角形,
综上所述,![]() 或
或![]() .
.

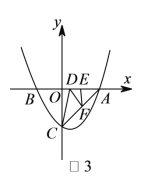
②i)当![]() 时,重叠部分为
时,重叠部分为![]() ,
,
∴![]() .
.
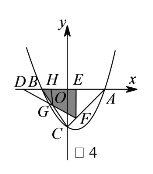
ii)当![]() 时,设
时,设![]() 与
与![]() 相交于点
相交于点![]() ,则重叠部分为四边形
,则重叠部分为四边形![]() ,如图
,如图![]() ,
,
过点![]() 作
作![]() 于
于![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() .
.
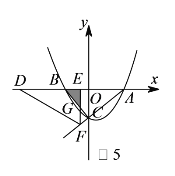
iii)当![]() 时,重叠部分为
时,重叠部分为![]() ,如图
,如图![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.