题目内容
【题目】如图，已知四边形ABCD是菱形，DF⊥AB于点F，BE⊥CD于点E．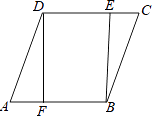
（1）求证：AF=CE；
（2）若DE=2，BE=4，求sin∠DAF的值．
【答案】
（1）证明：∵四边形ABCD是菱形，
∴AB∥CD，AB=CD，
∵DF⊥AB，BE⊥CD，
∴DF∥BE，
∴四边形BEDF是平行四边形，
∴BF=DE，
∴AF=CE；
（2）证明：∵DE=2，BE=4，
∴设AD=x，则AF=x﹣2，DF=BE=4，
在Rt△DAF中，x2=42+（x﹣2）2，
解得x=5，
∴sin∠DAF= 
= 
．
【解析】（1）判定四边形BEDF是平行四边形，根据平行四边形的对边相等，即可证得；（2）要求sin∠DAF，须求斜边BC的长，即菱形的边长，可在Rt△DAF中建立方程，求出AD，按照正弦定义即可求出.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识，掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半，以及对解直角三角形的理解，了解解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．
练习册系列答案
相关题目
