题目内容
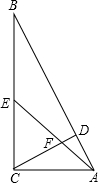 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=6,CD⊥AB于点D,点E是BC的中点,连接AE,AE与CD交于点F,则AF的长为________.
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=6,CD⊥AB于点D,点E是BC的中点,连接AE,AE与CD交于点F,则AF的长为________.

分析:过点F作FH⊥AC于H,则FH∥BC,所以△AFH∽AEC,设FH为x,由已知条件可证明△AHF是等腰直角三角形,所以AF=
 x,利用相似三角形的性质:对应边的比值相等即可得到关于x的方程,解方程求出x的值即可得到AF的长.
x,利用相似三角形的性质:对应边的比值相等即可得到关于x的方程,解方程求出x的值即可得到AF的长.解答:
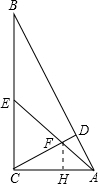 解:过点F作FH⊥AC于H,
解:过点F作FH⊥AC于H,∵∠ACB=90°,
∴BC⊥AC,
∴FH∥BC,
∴△AFH∽AEC,
∴
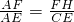 ,
,∵AC=3,BC=6,点E是BC的中点,
∴AC=CE=3,
∴△AEC是等腰直角三角形,
∴∠EAC=45°,AE=
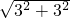 =3
=3
∴AH=FH,
设FH为x,则AH=x,∴AF=
 x,
x,∴
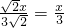 ,
,解得:x=1,
∴AF=
 ,
,故答案为:
 .
.点评:本题考查了相似是局限性的判定和性质、等腰直角三角形的判定和性质以及勾股定理的运用,解题的关键是做垂直,构造相似三角形.

练习册系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.