题目内容
10.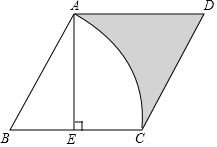 已知菱形ABCD中,E为BC的中点,AE⊥BC,BC=2$\sqrt{3}$,以点B为圆心,线段BA的长为半径作$\widehat{AC}$,则阴影部分的面积为( )
已知菱形ABCD中,E为BC的中点,AE⊥BC,BC=2$\sqrt{3}$,以点B为圆心,线段BA的长为半径作$\widehat{AC}$,则阴影部分的面积为( )| A. | 3$\sqrt{3}$-π | B. | 3$\sqrt{3}$-2π | C. | 6$\sqrt{3}$-2π | D. | 6$\sqrt{3}$-π |
分析 连接AC,结合线段垂直平分线的性质、菱形的性质判定△ABC是等边三角形,则图中阴影部分的面积=菱形的面积-扇形的面积.
解答  解:如图,连接AC,
解:如图,连接AC,
∵E为BC的中点,AE⊥BC,
∴AB=AC.
又在菱形ABCD中,AB=BC,
∴AB=AC=BC,
∴△ABC是等边三角形,
∴∠B=60°.
∵AB=BC=2$\sqrt{3}$,
∴BE=$\sqrt{3}$,
∴AE=3.
∴S阴影=S菱形ABCD-S扇形=BC•AE-$\frac{60π×(2\sqrt{3})^{2}}{360}$=6$\sqrt{3}$-2π.
故选:C.
点评 本题考查了扇形面积的计算,菱形的性质以及线段垂直平分线的性质.注意辅助线的作法和分割法求阴影部分的面积.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
1.小明买书需用34元钱,付款时恰好用了1元和5元的纸币共10张,设所用的1元纸币为x张,根据题意,下面所列方程正确的是( )
| A. | x+10(x-50)=34 | B. | x+5(10-x)=34 | C. | x+5(x-10)=34 | D. | 5x+(10-x)=34 |
15.计算(-3)×(-5)的结果是( )
| A. | 15 | B. | -15 | C. | 8 | D. | -8 |
19.在平面直角坐标系中,点A的坐标为(-1,2),点B的坐标为(5,4),则线段AB的中点坐标为( )
| A. | (2,3) | B. | (2,2.5) | C. | (3,3) | D. | (3,2.5) |