题目内容
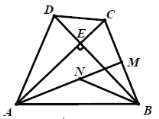
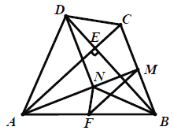
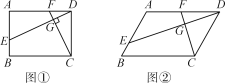
【题目】如图,把两个全等的矩形![]() 和矩形
和矩形![]() 拼成如图所示的图案,连接
拼成如图所示的图案,连接![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转,点
逆时针旋转,点![]() 的运动轨迹交
的运动轨迹交![]() 于点
于点![]() ,若
,若![]() ,有以下四个结论:①
,有以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④阴影部分的面积为
;④阴影部分的面积为![]() .其中一定成立的是______.(把所有正确结论的序号填在横线上)
.其中一定成立的是______.(把所有正确结论的序号填在横线上)
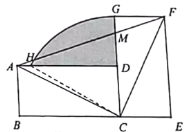
【答案】①③④
【解析】
根据四边形ABCD,EFGC为全等的矩形,得到AB=CE,∠B=∠E=90°,BC=EF,即可得到△ABC≌△CEF,根据全等的性质得到∠ACB=∠CFE,AC=CF,可得![]() 同理可证△ABC≌△FGC (SAS) ,可判别②错误,利用平行线段成比例可得
同理可证△ABC≌△FGC (SAS) ,可判别②错误,利用平行线段成比例可得![]() ,可求出MD的长,即可得出
,可求出MD的长,即可得出![]() ,进行判断③
,进行判断③
;利用![]() 可计算出阴影部分面积,进行判断④
可计算出阴影部分面积,进行判断④
证明: (1)∵四边形ABCD,EFGC为全等的矩形,
∴AB= CE,∠B=∠E= 90°BC= EF
在△ABC和△CEF中,
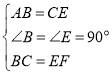
∴△ABC≌△CEF(SAS) ,
∴∠ACB=∠CFE,AC= CF
∴![]()
故①正确,
∵四边形ABCD,EF GC为全等的矩形,
∴AB= GF,∠B=∠CGF= 90°BC= CG
在△ABC和△FGC中,
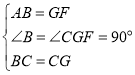
∴△ABC≌△FGC (SAS) ,
故②错误,
∵GF//AD
∴![]()
∵CG=4,CD=2
∴GD=2
∴![]()
在Rt△ADM中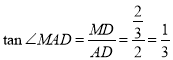
故③正确;
∵四边形ABCD是矩形,
∴AD=BC=4,CD=AB=2,∠BCD=∠ADC=90°,
∴CH=BC=4,CH=2CD.
∴∠DHC=30°,
∴∠DCH=60°.
由勾股定理得DE=![]()
∴![]()
故④正确
故答案为:①③④

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
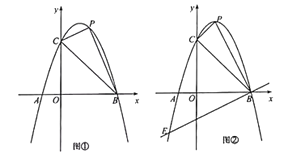
小学教材完全解读系列答案【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.