题目内容
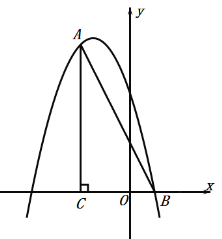
【题目】如图①,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 为抛物线第一象限上一动点,连接
为抛物线第一象限上一动点,连接![]() 、
、![]() 、
、![]() .
.
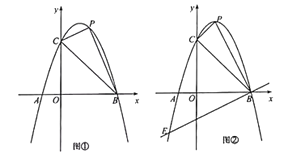
(1)求抛物线的解析式,并直接写出抛物线的顶点坐标;
(2)当![]() 的面积最大时,求出点
的面积最大时,求出点![]() 的坐标;
的坐标;
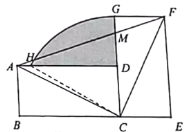
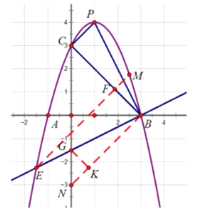
(3)如图②,当点![]() 与抛物线顶点重合时,过点
与抛物线顶点重合时,过点![]() 的直线
的直线![]() 与抛物线交于点
与抛物线交于点![]() ,在直线
,在直线![]() 上方的抛物线上是否存在一点
上方的抛物线上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,顶点坐标为
,顶点坐标为![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)存在,点
;(3)存在,点![]() 的坐标为
的坐标为![]() ,理由见解析
,理由见解析
【解析】
(1 )只需运用待定系数法就可求出二次函数的解析式,运用配方法就可求出抛物线的顶点坐标;
(2) 过点![]() 作
作![]() 轴,交线段
轴,交线段![]() 于点
于点![]() ,直线
,直线![]() 的表达式为:
的表达式为:![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 坐标为
坐标为![]() ,得出
,得出![]() ;可得
;可得![]() ,即可求出
,即可求出![]() 的面积最大时点
的面积最大时点![]() 的坐标;
的坐标;
(3)
在![]() 轴上取
轴上取![]() ,连接
,连接![]() ,过直线
,过直线![]() 与
与![]() 轴的交点
轴的交点![]() 作
作![]() .利用勾股逆定理可得
.利用勾股逆定理可得![]() 为直角三角形,
为直角三角形,![]() ,故
,故![]() ,求出直线
,求出直线![]() 的表达式为
的表达式为![]() ,且点
,且点![]() 坐标为
坐标为![]() ,联立
,联立 即可得点
即可得点![]() 的坐标为
的坐标为![]() .解得:
.解得:![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,故
,故![]() ,得出
,得出![]() ,求出直线
,求出直线![]() 的表达式为
的表达式为![]() ,及直线
,及直线![]() 的表达式为
的表达式为![]() 联立
联立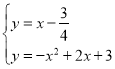 可得点
可得点![]() 的坐标.
的坐标.
(1)将![]() 、
、![]() 代入
代入![]() 得:
得:
![]() ,
,
解得:![]() .
.
∴抛物线的解析式为![]() .
.
∴![]()
∴顶点坐标为![]() .
.
(2)过点![]() 作
作![]() 轴,交线段
轴,交线段![]() 于点
于点![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
设直线![]() 的表达式为
的表达式为![]() ,
,
将![]() 、
、![]() 代入得:
代入得:
![]() ,解得:
,解得:![]() .
.
∴直线![]() 的表达式为
的表达式为![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 坐标为
坐标为![]() ,
,
∴![]() ;
;
∴![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() .
.
∴此时![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.

(3)存在.
在![]() 轴上取
轴上取![]() ,连接
,连接![]() ,过直线
,过直线![]() 与
与![]() 轴的交点
轴的交点![]() 作
作![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 为直角三角形,
为直角三角形,![]() ,
,
∴![]() ,
,
∵直线![]() 过点
过点![]() ,
,
∴![]() ,解得:
,解得:![]() .
.
∴直线![]() 的表达式为
的表达式为![]() ,且点
,且点![]() 坐标为
坐标为![]() ,
,
由 ,解得:
,解得:![]() 或
或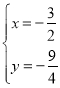 ,
,
即点![]() 的坐标为
的坐标为![]() .
.
解得:![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴直线![]() 的表达式为
的表达式为![]() ,
,
∴设直线![]() 的表达式为
的表达式为![]() ,
,
将点![]() 代入得:
代入得:![]() ,解得:
,解得:![]() .
.
∴设直线![]() 的表达式为
的表达式为![]() .
.
由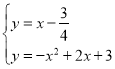 解得:
解得:![]() 或
或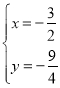 ,
,
即点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目