题目内容
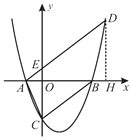
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(A点在B点的左边),与
两点(A点在B点的左边),与![]() 轴交于点
轴交于点![]() .
.
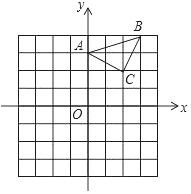
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
(2)如图1,在(1)的条件下,点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,若以
在抛物线的对称轴上,若以![]() 为边,以点
为边,以点![]() 、
、![]() 、
、![]() 、Q为顶点的四边形是平行四边形,求
、Q为顶点的四边形是平行四边形,求![]() 点的坐标;
点的坐标;
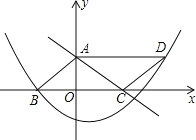
(3)如图2,过点![]() 作直线
作直线![]() 的平行线交抛物线于另一点
的平行线交抛物线于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() ﹕
﹕![]() =1﹕4. 求
=1﹕4. 求![]() 的值.
的值.
【答案】(1) ![]() ;(2)
;(2) ![]() 和
和![]()
![]() ;(3)
;(3) ![]()
【解析】
(1)设![]() ,
,![]() ,再根据根与系数的关系得到
,再根据根与系数的关系得到![]() ,根据勾股定理得到:
,根据勾股定理得到:![]() 、
、 ![]() ,根据
,根据![]() 列出方程,解方程即可;(2)求出A、B坐标,设出点Q坐标,利用平行四边形的性质,分类讨论点P坐标,利用全等的性质得出P点的横坐标后,分别代入抛物线解析式,求出P点坐标;
列出方程,解方程即可;(2)求出A、B坐标,设出点Q坐标,利用平行四边形的性质,分类讨论点P坐标,利用全等的性质得出P点的横坐标后,分别代入抛物线解析式,求出P点坐标;
(3)过点![]() 作DH⊥
作DH⊥![]() 轴于点
轴于点![]() ,由
,由![]() :
:![]() :
:![]() ,可得
,可得![]() :
:![]() :
:![]() .设
.设![]() ,可得
,可得 ![]() 点坐标为
点坐标为![]() ,可得
,可得![]() .设
.设![]() 点坐标为
点坐标为![]() .可证△
.可证△![]() ∽△
∽△![]() ,利用相似性质列出方程整理可得到
,利用相似性质列出方程整理可得到 ![]() ①,将
①,将![]() 代入抛物线上,可得
代入抛物线上,可得![]() ②,联立①②解方程组,即可解答.
②,联立①②解方程组,即可解答.
解:![]() 设
设![]() ,
,![]() ,则
,则![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() .
.
∵已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
∴![]()
在![]() △
△![]() 中:
中:![]() ,在
,在![]() △
△![]() 中:
中:![]() ,
,
∵△![]() 为直角三角形,由题意可知∠
为直角三角形,由题意可知∠![]() °,
°,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
又![]() ,
,
∴![]() .
.
![]() 由
由![]() 可知:
可知:![]() ,令
,令![]() 则
则![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.
①以![]() 为边,以点
为边,以点![]() 、
、![]() 、
、![]() 、Q为顶点的四边形是四边形
、Q为顶点的四边形是四边形![]() 时,
时,
设抛物线的对称轴为![]() ,l与
,l与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ⊥l,垂足为点
⊥l,垂足为点![]() ,
,
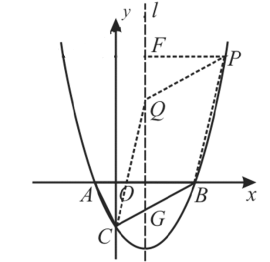
即∠![]() °
°![]() ∠
∠![]() .
.
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ∥
∥![]() ,又l∥
,又l∥![]() 轴,
轴,
∴∠![]() ∠
∠![]() =∠
=∠![]() ,
,
∴△![]() ≌△
≌△![]() ,
,
∴![]() ,
,
∴![]() 点的横坐标为
点的横坐标为![]() ,
,
∴![]()
即![]() 点坐标为
点坐标为![]() .
.
②当以![]() 为边,以点
为边,以点![]() 、
、![]() 、
、![]() 、Q为顶点的四边形是四边形
、Q为顶点的四边形是四边形![]() 时,
时,
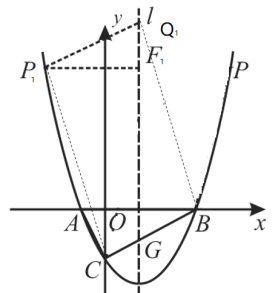
设抛物线的对称轴为![]() ,l与
,l与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ⊥l,垂足为点
⊥l,垂足为点![]() ,
,
即∠![]() °
°![]() ∠
∠![]() .
.
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ∥
∥![]() ,又l∥
,又l∥![]() 轴,
轴,
∴∠![]() ∠
∠![]() =∠
=∠![]() ,
,
∴△![]() ≌△
≌△![]() ,
,
∴![]() ,
,
∴![]() 点的横坐标为
点的横坐标为![]() ,
,
∴![]()
即![]() 点坐标为
点坐标为![]()
∴符合条件的![]() 点坐标为
点坐标为![]() 和
和![]() .
.
![]() 过点
过点![]() 作DH⊥
作DH⊥![]() 轴于点
轴于点![]() ,
,
∵![]() :
:![]() :
:![]() ,
,
∴![]() :
:![]() :
:![]() .
.
设![]() ,则
,则![]() 点坐标为
点坐标为![]() ,
,
∴![]() .
.
∵![]() 点在抛物线
点在抛物线![]() 上,
上,
∴![]() 点坐标为
点坐标为![]() ,
,
由(1)知![]() ,
,
∴![]() ,
,
∵![]() ∥
∥![]() ,
,
∴△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
∴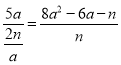 ,
,
即![]() ①,
①,
又![]() 在抛物线上,
在抛物线上,
∴![]() ②,
②,
将代入①得:![]() ,
,
解得![]() (舍去),
(舍去),![]()
把![]() 代入②得:
代入②得:![]() .
.

【题目】书籍是人类进步的阶梯,联合国教科文组织把每年的4月23日确定为“世界读书日”,某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:一个学期平均一天阅读课外书籍所有时间统计表
时间(分钟) | 20 | 40 | 60 | 80 | 100 | 120 |
人数 | 43 | 31 | 15 | 5 | 4 | 2 |
请你根据以上信息解答下列问题:
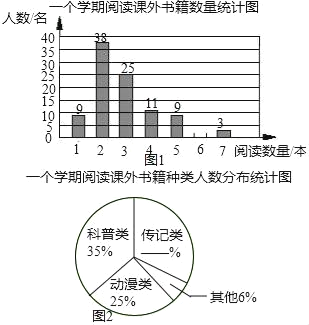
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有1200名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.