Question

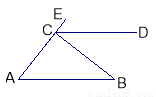
如图，在直角坐标系xoy中，O是坐标原点，点A在x正半轴上，OA=cm，点B在y轴的正半轴上，OB=12cm，动点P从点O开始沿OA以cm/s的速度向点A移动，动点Q从点A开始沿AB以4cm/s的速度向点B移动，动点R从点B开始沿BO以2cm/s的速度向点O移动．如果P、Q、R分别从O、A、B同时移动，移动时间为t（0＜t＜6）s．

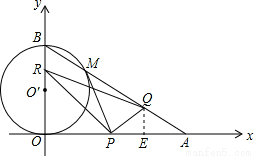
（1）求∠OAB的度数．

（2）以OB为直径的⊙O‘与AB交于点M，当t为何值时，PM与⊙O‘相切？

（3）求出△PQR的面积S随动点移动时间t的函数关系式，并求s的最小值及相应的t值．

 

Answer 1

（1）30°；（2）3；（3）3．

【解析】

试题分析：（1）在Rt△OAB中，已知了OA、OB的长，即可求出∠OAB的正切值，由此可得到∠OAB的度数；

（2）连接O′M，当PM与⊙O′相切时，PM、PO同为⊙O′的切线，易证得△OO′P≌△MO′P，则∠OO′P=∠MO′P；在（1）中易得∠OBA=60°，即△O′BM是等边三角形，由此可得到∠BO′M=∠PO′M=∠PO′O=60°；在Rt△OPO′中，根据∠PO′O的度数及OO′的长即可求得OP的长，已知了P点的运动速度，即可根据时间=路程÷速度求得t的值；

（3）过Q作QE⊥x轴于E，在Rt△AQE中，可用t表示出AQ的长，进而根据∠OAB的度数表示出QE、AE的长，由S△PQR=S△OAB-S△OPR-S△APQ-S△BRQ即可求得S、t的函数关系式；根据所得函数的性质及自变量的取值范围即可求出S的最小值及对应的t的值．

试题解析：（1）在Rt△AOB中：

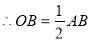
∴∠OAB=30°

（2）如图，连接O‘P，O‘M．当PM与⊙O‘相切时，

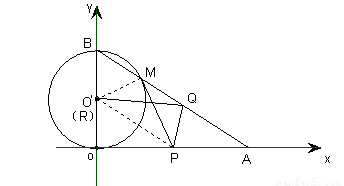
有∠PM O‘=∠PO O‘=90°，

△PMO‘≌△POO‘由（1）知∠OBA=60°

∵O‘M= O‘B ∴△O‘BM是等边三角形

∴∠B O‘M=60°

可得∠O O‘P=∠M O‘P=60°

∴

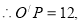
OP=

又∵OP=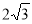t

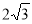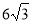∴t=，t=3

即：t=3时，PM与⊙O‘相切

（3）如图，过点Q作QE⊥x于点E

∵∠BAO=30°，AQ=4t

∴QE=AQ=2t AE=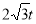

∴OE=OA-AE=-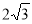t

∴Q点的坐标为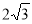（-t，2t）

S=S△PQR= S△OAB -S△OPR -S△APQ -S△BRQ

=

= （）

∵S== （）

双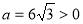,抛物线开口向上

∴当t=3时，S最小值=

考点：圆的综合题．