题目内容
计算或解方程
(1)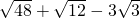 ;
;
(2)x2+4x-5=0.
解:(1)原式=4 +2
+2 -3
-3
=3 ;
;
(2)∵x2+4x-5=0,
∴(x+5)(x-1)=0,
∴x+5=0或x-1=0,
解得:x1=-5,x2=1.
分析:(1)首先将各二次根式化为最简二次根式,然后合并同类二次根式即可求得答案;
(2)利用十字相乘法分解因式的知识,即可将原式化为:(x+5)(x-1)=0,继而求得答案.
点评:此题考查了二次根式的加减运算与因式分解法解一元二次方程的知识.此题比较简单,注意二次根式需化为最简二次根式,注意掌握十字相乘法分解因式的知识是解此题的关键.
 +2
+2 -3
-3
=3
 ;
;(2)∵x2+4x-5=0,
∴(x+5)(x-1)=0,
∴x+5=0或x-1=0,
解得:x1=-5,x2=1.
分析:(1)首先将各二次根式化为最简二次根式,然后合并同类二次根式即可求得答案;
(2)利用十字相乘法分解因式的知识,即可将原式化为:(x+5)(x-1)=0,继而求得答案.
点评:此题考查了二次根式的加减运算与因式分解法解一元二次方程的知识.此题比较简单,注意二次根式需化为最简二次根式,注意掌握十字相乘法分解因式的知识是解此题的关键.

练习册系列答案
相关题目