题目内容
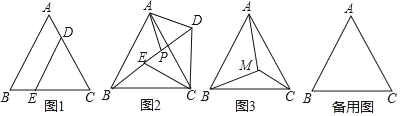
【题目】如图,边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2![]() .
.
(1)若将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD,BE,在旋转过程中,AD和BE又怎样的数量关系?并说明理由;
(2)在(1)旋转过程中,边D′E′的中点为P,连接AP,当AP最大时,求AD′的值.
(3)若点M为等边△ABC内一点,且MA=4a,MB=5a,MC=3a,求∠AMC的度数.
【答案】(1)AD'=BE',理由见解析;(2)2![]() ;(3)∠AMC=150°.
;(3)∠AMC=150°.
【解析】试题分析:(1)利用旋转的性质,即可判断出△ACD≌△BCE'即可得出结论;
(2)先判断出点A,C,P三点共线,先求出CP,AP,最后用勾股定理即可得出结论;
(3)将△BMC绕点C顺时针旋转得到△ANC,连接MN,只要证明△CMN是等边三角形,△AMN是Rt△即可解决问题;
试题解析:(1)结论:AD'=BE',
理由:当α≠180°时,由旋转的性质得,∠ACD'=∠BCE',
由(1)知,AC=BC,CD'=CE',
∴△ACD'≌△BCE',
∴AD'=BE';
(2)如图连接CP,
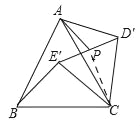
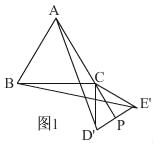
在△ACP中,由三角形三边关系得,AP<AC+CP,
∴当点A,C,P三点共线时,AP最大,
如图1,在△D'CE'中,由P为D'E的中点,得AP⊥D'E',PD'=![]() ,
,
∴CP=3,
∴AP=6+3=9,
在Rt△APD'中,由勾股定理得,AD'=![]() =2
=2![]() ;
;
(3)将△BMC绕点C顺时针旋转得到△ANC,连接MN,
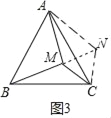
∴CM=CN,BM=AN,△BCM≌△ACN,
∵ABC是等边三角形,
∴∠ACB=60°,
∵∠ACN=∠BCM,
∴∠MCN=60°,
∴△CMN是等边三角形,
∴∠CMN=60°,MN=CM=6,
在△AMN中,∵AM2+MN2=(4a)2+(3a)2=(5a)2=AN2,
∴∠AMN=90°,
∴∠AMC=150°.