题目内容
 如图,Rt△ABC中,∠C=90°,⊙O内切于Rt△ABC,AC边切⊙O于点D,若AC=4,BC=3,则tan∠CAO的值为
如图,Rt△ABC中,∠C=90°,⊙O内切于Rt△ABC,AC边切⊙O于点D,若AC=4,BC=3,则tan∠CAO的值为
- A.

- B.

- C.

- D.

A
分析:根据直角三角形内切圆的性质得出内切圆半径,再利用正方形的判定得出四边形ODCE是正方形,进而得出tan∠CAO的值为: =
= .
.
解答: 解:设BC切⊙O于点E,连接OE,设⊙O的半径是r,
解:设BC切⊙O于点E,连接OE,设⊙O的半径是r,
由勾股定理得:AB= =5,
=5,
∵⊙O是三角形ABC的内切圆,
∴r=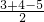 =1,
=1,
即OD=1,
∵⊙O内切于Rt△ABC,AC边切⊙O于点D,BC切⊙O于点E,
∴OE⊥BC,OD⊥AC,
∵∠C=90°,
∴四边形ODCE是矩形,
∵OE=OD,
∴四边形ODCE是正方形,
∴AD=AC-CD=4-1=3,
则tan∠CAO的值为: =
= .
.
故选:A.
点评:此题主要考查了直角三角形内切圆半径求法以及正方形的判定,根据已知得出AD以及DO的长是解题关键.
分析:根据直角三角形内切圆的性质得出内切圆半径,再利用正方形的判定得出四边形ODCE是正方形,进而得出tan∠CAO的值为:
 =
= .
.解答:
 解:设BC切⊙O于点E,连接OE,设⊙O的半径是r,
解:设BC切⊙O于点E,连接OE,设⊙O的半径是r,由勾股定理得:AB=
 =5,
=5,∵⊙O是三角形ABC的内切圆,
∴r=
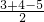 =1,
=1,即OD=1,
∵⊙O内切于Rt△ABC,AC边切⊙O于点D,BC切⊙O于点E,
∴OE⊥BC,OD⊥AC,
∵∠C=90°,
∴四边形ODCE是矩形,
∵OE=OD,
∴四边形ODCE是正方形,
∴AD=AC-CD=4-1=3,
则tan∠CAO的值为:
 =
= .
.故选:A.
点评:此题主要考查了直角三角形内切圆半径求法以及正方形的判定,根据已知得出AD以及DO的长是解题关键.

练习册系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.