题目内容
12.如图①是一张矩形台球桌,图②是台球桌的平面图.其中A、B、C、D处分别有球洞,已知DE=4,CE=2,BC=6$\sqrt{3}$,球从E点出发,与DC夹角为α,经过BC、AB、AD三次反弹后回到E点,则EF=4.(结果精确到1,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 根据球的运动轨迹可知四个三角形相似,并且相对的两个三角形全等,由于DE=4,CE=2,设CF=x,则BF=6$\sqrt{3}$-x,由△BGF∽△CEF,可得$\frac{BG}{EC}$=$\frac{BF}{FC}$,列出方程即可解决问题.
解答 解:如图: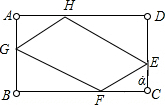
∵DE=4,CE=2,球从E点出发,与DC夹角为α,经过BC、AB、AD三次反弹后回到E点,
∴四个三角形相似,并且相对的两个三角形全等,设CF=x,则BF=6$\sqrt{3}$-x,
∵△BGF∽△CEF,
∴$\frac{BG}{EC}$=$\frac{BF}{FC}$,
∴$\frac{4}{2}$=$\frac{6\sqrt{3}-x}{x}$,
∴x=2$\sqrt{3}$,
∴EF=$\sqrt{E{C}^{2}+C{F}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4.
故答案为4.
点评 考查了解直角三角形的应用,解题的关键是根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

练习册系列答案
相关题目
10.有理数-$\frac{1}{5}$的倒数为( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | $-\frac{1}{5}$ | D. | -5 |
17.一组数据:3、-1、0、2、-3、4,则这组数据的中位数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 2.5 |
4.若代数式$\frac{2}{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x<2 | B. | x≠2 | C. | x>2 | D. | x=2 |
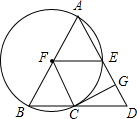 如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.