题目内容
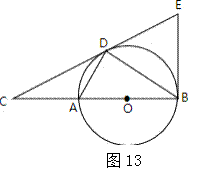
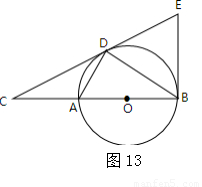
.如图13,D为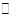 O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是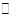 O的切线;
O的切线;
(2)过点B作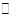 O的切线交CD的延长线于点E,若BC=6,tan∠CDA=
O的切线交CD的延长线于点E,若BC=6,tan∠CDA= ,求BE的长
,求BE的长
【答案】
(1)证明:连OD,OE,如图,
∵AB为直径,
 ∴∠ADB=90°,即∠ADO+∠1=90°,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,
∴ED=EB,OD⊥BD,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA= ,
,
∴tan∠OEB= ,
,
∵Rt△CDO∽Rt△CBE,
∴ ,
,
∴CD= ,
,
在Rt△CBE中,设BE= ,
,
∴ ,
,
解得 .
.
即BE的长为 .
.
【解析】略

练习册系列答案
相关题目
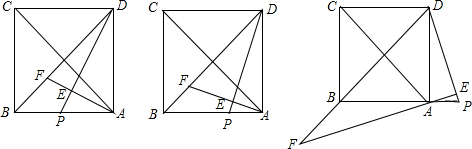
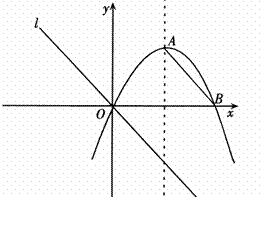
 O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.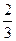 ,求BE的长
,求BE的长