题目内容
如图,在边长为6的正方形ABCD中,点P为AB上一动点,连接DB、DP,AE⊥DP于E.(1)如图①,若P为AB的中点,则
| BF |
| DF |
| BF |
| AC |
(2)如图②,若
| AP |
| BP |
| 1 |
| 2 |
(3)如图③,若P在BA的延长线上,当
| BF |
| AC |
| AP |
| AB |
| 1 |
| 3 |
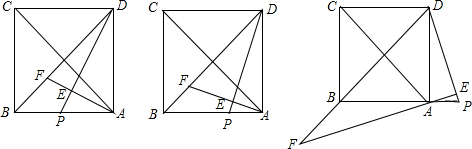
分析:(1)延长AF交BC于M,证△ABM≌△DAP,得BM=AP,再根据△MBF∽△ADF对应边成比例列出比例式
=
=
,然后再根据正方形的边长相等,对角线相等进行转化即可求解;
(2)先根据已知条件求出
=
,然后同(1)的方法作出辅助线即可进行证明;
(3)同前两小题的思路,延长CB交AF于点M,然后同(1)的求解思路进行求解计算.
| BF |
| DF |
| BM |
| AD |
| BF |
| FD |
(2)先根据已知条件求出
| AP |
| AB |
| 1 |
| 3 |
(3)同前两小题的思路,延长CB交AF于点M,然后同(1)的求解思路进行求解计算.
解答:解:(1)延长AF交BC于M,
∴∠BAM+∠AMB=90°
∵AE⊥DP,
∴∠BAM+∠DPA=90°,
∴∠AMB=∠DPA,
在△ABM≌△DAP中,
,
∴△ABM≌△DAP(AAS),
∴AP=BM(全等三角形对应边相等),
∵四边形ABCD是正方形,
∴BC∥AD,
∴△MBF∽△ADF,
∴
=
,
∵点P是AB的中点,
∴AP=BM=
AB=
AD,
∴
=
=
=
,
∴
=
=
,
即
=
,
又∵AC=BD,
∴
=
;
故答案为:
,
;

(2)∵
=
,
∴
=
=
,
即
=
,
方法同(1),延长AF交BC于M,
则
=
=
=
,
∴
=
=
,
即
=
,
∵正方形的对角线AC=BD,
∴
=
,
∴AC=4BF;
(3)延长CB交AF于点M,方法同(1)可得
=
=
,
∴
=
,
∴
=
,
即
=
,
∵正方形的对角线AC=BD,
∴
=
.
故答案为:
.
∴∠BAM+∠AMB=90°
∵AE⊥DP,
∴∠BAM+∠DPA=90°,
∴∠AMB=∠DPA,
在△ABM≌△DAP中,
|
∴△ABM≌△DAP(AAS),
∴AP=BM(全等三角形对应边相等),
∵四边形ABCD是正方形,
∴BC∥AD,
∴△MBF∽△ADF,
∴
| BF |
| DF |
| BM |
| AD |
∵点P是AB的中点,
∴AP=BM=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| BF |
| DF |
| BM |
| AD |
| BF |
| FD |
| 1 |
| 2 |
∴
| BF |
| FD+BF |
| 1 |
| 1+2 |
| 1 |
| 3 |
即
| BF |
| FD |
| 1 |
| 3 |
又∵AC=BD,
∴
| BF |
| AC |
| 1 |
| 3 |
故答案为:
| 1 |
| 2 |
| 1 |
| 3 |

(2)∵
| AP |
| BP |
| 1 |
| 2 |
∴
| AP |
| AP+BP |
| 1 |
| 1+2 |
| 1 |
| 3 |
即
| AP |
| AB |
| 1 |
| 3 |
方法同(1),延长AF交BC于M,
则
| BM |
| AD |
| AP |
| AB |
| BF |
| FD |
| 1 |
| 3 |
∴
| BF |
| BF+FD |
| 1 |
| 1+3 |
| 1 |
| 4 |
即
| BF |
| BD |
| 1 |
| 4 |
∵正方形的对角线AC=BD,
∴
| BF |
| AC |
| 1 |
| 4 |
∴AC=4BF;
(3)延长CB交AF于点M,方法同(1)可得
| BM |
| AD |
| AP |
| AB |
| 1 |
| 3 |
∴
| BF |
| FD |
| 1 |
| 3 |
∴
| BF |
| FD-BF |
| 1 |
| 3-1 |
即
| BF |
| BD |
| 1 |
| 2 |
∵正方形的对角线AC=BD,
∴
| BF |
| AC |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了正方形的性质,相似三角形的判定与相似三角形的性质,全等三角形的判定与性质,此类题目往往是后面的小题的解题思路继续沿用第(1)小题的思路,所以找准第(1)小题的求解思路很重要.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
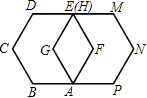 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( ) 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.