题目内容
正△ABC内接于⊙O,M、N分别是AB、AC的中点,延长MN交⊙O于点D,连接BD交AC于P,则| PC | PA |
分析:可延长NM交⊙O于E,设正三角形边长为a,ND=x,由相交弦定理,得ND•NE=AN•NC,代入得出x与a的比值,再由△PDN∽△PBC,得出其对应边成比例,进而通过线段之间的转化,即可得出结论.
解答: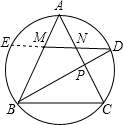 解:如图所示,延长NM交⊙O于E,设正三角形边长为a,ND=x,
解:如图所示,延长NM交⊙O于E,设正三角形边长为a,ND=x,
由相交弦定理,得ND•NE=AN•NC,
即x(
+x)=
•
,
x2+
x-
=0
∴x=
(
-1)?
=
,
又△PDN∽△PBC,∴
=
=
=
,
∴
=
?
=
,
∵2•PN+PC=PN+(PN+PC)=PN+NC=PN+NA=PA,
∴
=
.
故答案为:
.
 解:如图所示,延长NM交⊙O于E,设正三角形边长为a,ND=x,
解:如图所示,延长NM交⊙O于E,设正三角形边长为a,ND=x,由相交弦定理,得ND•NE=AN•NC,
即x(
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
x2+
| a |
| 2 |
| a2 |
| 4 |
∴x=
| a |
| 4 |
| 5 |
| x |
| a |
| ||
| 4 |
又△PDN∽△PBC,∴
| PN |
| PC |
| ND |
| BC |
| x |
| a |
| ||
| 4 |
∴
| 2PN |
| PC |
| ||
| 2 |
| 2PN+PC |
| PC |
| ||
| 2 |
∵2•PN+PC=PN+(PN+PC)=PN+NC=PN+NA=PA,
∴
| PC |
| PA |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题主要考查了相似三角形的判定及性质以及相交弦定理的运用,能够利用其性质建立线段之间的联系,进而解题.

练习册系列答案
相关题目
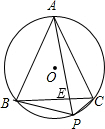 如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:①PA=PB+PC;②
如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:①PA=PB+PC;② 如图,正△ABC内接于半径为1cm的圆,则阴影部分的面积为
如图,正△ABC内接于半径为1cm的圆,则阴影部分的面积为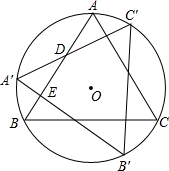 (2013•江东区模拟)如图,圆O的半径为R,正△ABC内接于圆O,将△ABC按逆时针方向旋转90°后得到△A′B′C′,它的两边与AB相交于点D、E,则以下说法正确的个数是( )
(2013•江东区模拟)如图,圆O的半径为R,正△ABC内接于圆O,将△ABC按逆时针方向旋转90°后得到△A′B′C′,它的两边与AB相交于点D、E,则以下说法正确的个数是( ) 如图,正△ABC内接于⊙O,D是⊙O上一点,∠DCA=15°,CD=10,则BC的长为( )
如图,正△ABC内接于⊙O,D是⊙O上一点,∠DCA=15°,CD=10,则BC的长为( )