题目内容
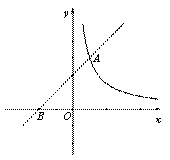
如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.
(1)求证:∠E=∠C;
(2)当⊙O的半径为3,cosA= 时,求EF的长.
时,求EF的长.

(1) 证明:连接OB
 CD为⊙O的直径
CD为⊙O的直径



 AE是⊙O的切线. .
AE是⊙O的切线. .




 OB、OC是⊙O的半径
OB、OC是⊙O的半径
 OB=OC
OB=OC


 OE∥BD,
OE∥BD,




(2)解:  在Rt△
在Rt△ 中,cosA=
中,cosA= ,OB=3
,OB=3


 AD=2 . .
AD=2 . .

 BD//OE
BD//OE




 . .
. .
 OE∥BD,
OE∥BD,


 在Rt△
在Rt△ 中,tanE=
中,tanE=
 在Rt△
在Rt△ 中,tanE=
中,tanE=
设FB为x





 (舍负)
(舍负)

 EF= . .
EF= . .

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的绝对值是
的绝对值是  B.
B. D.
D.
 倍,求:甲、乙两班各有多少名学生。
倍,求:甲、乙两班各有多少名学生。 有意义,那么
有意义,那么 的取值范围是 .
的取值范围是 .
 B.
B. C. -5 D.5
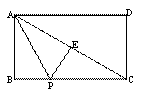
C. -5 D.5  ,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是
,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是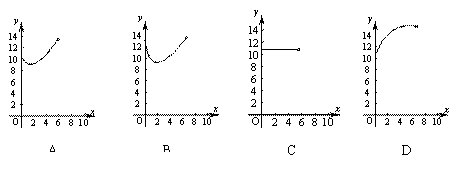
 的绝对值是
的绝对值是 C.
C. D.
D.
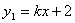 的图象与
的图象与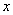 轴交于点
轴交于点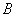 (
(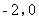 ),与函数
),与函数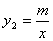 (
( )的图象交于点
)的图象交于点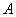 (
(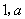 ).
).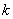 和
和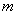 的值;
的值;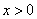 )的图象沿
)的图象沿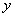 轴向下平移3个单位后交x轴于点
轴向下平移3个单位后交x轴于点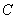 .若点
.若点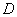 是平移后函数图象上一点,且△
是平移后函数图象上一点,且△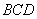 的面积是3,直接写出点
的面积是3,直接写出点