题目内容
设点P的坐标(x,y),根据下列条件判定点P在坐标平面内的位置:
(1)xy=0;
(2)xy>0;
(3)x+y=0.
解:(1)∵xy=0,
∴x=0或y=0,
∴P点在坐标轴上;
(2)∵xy>0,
∴x、y同号,
∴P点在第一或第三象限;
(3)∵x+y=0,
∴x、y互为相反数,
∴P点在二、四象限内两坐标轴夹角的平分线上.
分析:(1)根据0乘以任何数都等于0判断出x=0或y=0,然后根据坐标轴上点的坐标特征解答;
(2)根据同号得正判断出x、y同号,再根据各象限内点的坐标特征解答;
(3)根据互为相反数的两个数的和等于0判断出x、y互为相反数,然后解答.
点评:本题考查了点坐标,熟记坐标轴上与各象限内点的坐标特征是解题的关键.
∴x=0或y=0,
∴P点在坐标轴上;
(2)∵xy>0,
∴x、y同号,
∴P点在第一或第三象限;
(3)∵x+y=0,
∴x、y互为相反数,
∴P点在二、四象限内两坐标轴夹角的平分线上.
分析:(1)根据0乘以任何数都等于0判断出x=0或y=0,然后根据坐标轴上点的坐标特征解答;
(2)根据同号得正判断出x、y同号,再根据各象限内点的坐标特征解答;
(3)根据互为相反数的两个数的和等于0判断出x、y互为相反数,然后解答.
点评:本题考查了点坐标,熟记坐标轴上与各象限内点的坐标特征是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
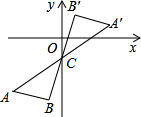 如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )
如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,设点A′的坐标为(a,b),则点A的坐标为( )| A、(-a,-b) | B、(-a,-b-1) | C、(-a,-b+1) | D、(-a,-b-2) |
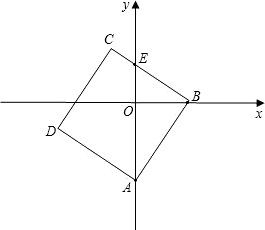 BCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m.
BCD某一边的交点,设点B的坐标为(t,0),线段OE的长度为m. 置关系时的m的取值范围;
置关系时的m的取值范围; 如图,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).
如图,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).