题目内容
 有一块锐角三角形余料ABC,它的边BC=12cm,BC边上的高为9cm,现要把它分割成若干个邻边长分别为4cm和2cm的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为4cm的边在BC上,则按如图方式分割成的小长方形零件最多有
有一块锐角三角形余料ABC,它的边BC=12cm,BC边上的高为9cm,现要把它分割成若干个邻边长分别为4cm和2cm的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为4cm的边在BC上,则按如图方式分割成的小长方形零件最多有
- A.3个
- B.4个
- C.5个
- D.6个
B
分析:如图作EF交BA、BC于点E、F,得到EF∥BC,利用相似三角形求得GD的长,进而可以求得可以裁几层这样的长方形,从而得到答案.
解答: 解:如图当最上层的小长方形的一边与AB、AC交于点E、F时,
解:如图当最上层的小长方形的一边与AB、AC交于点E、F时,
EF∥BC,
∴△AEF∽△ABC,
∴
∵BC=12cm,AD=9cm,小正方形邻边长分别为4cm和2cm
∴
解得:AG=3,
∴GD=6cm,
∵小正方形的宽为2cm,
∴能分割三层小长方形,
∵BC=12cm,
∴最底层能裁两个小长方形,
故共裁4个小长方形.
故选B.
点评:本题考查了相似三角形的应用,利用条件得到相似三角形并利用相似三角形的性质求得ED的长是解决本题的关键.
分析:如图作EF交BA、BC于点E、F,得到EF∥BC,利用相似三角形求得GD的长,进而可以求得可以裁几层这样的长方形,从而得到答案.
解答:
 解:如图当最上层的小长方形的一边与AB、AC交于点E、F时,
解:如图当最上层的小长方形的一边与AB、AC交于点E、F时,EF∥BC,
∴△AEF∽△ABC,
∴

∵BC=12cm,AD=9cm,小正方形邻边长分别为4cm和2cm
∴

解得:AG=3,
∴GD=6cm,
∵小正方形的宽为2cm,
∴能分割三层小长方形,
∵BC=12cm,
∴最底层能裁两个小长方形,
故共裁4个小长方形.
故选B.
点评:本题考查了相似三角形的应用,利用条件得到相似三角形并利用相似三角形的性质求得ED的长是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
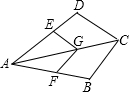
 有一块锐角三角形余料ABC,它的边BC=12cm,BC边上的高为9cm,现要把它分割成若干个邻边长分别为4cm和2cm的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为4cm的边在BC上,则按如图方式分割成的小长方形零件最多有( )
有一块锐角三角形余料ABC,它的边BC=12cm,BC边上的高为9cm,现要把它分割成若干个邻边长分别为4cm和2cm的小长方形零件,分割方式如图所示(分割线的耗料不计),使最底层的小方形的长为4cm的边在BC上,则按如图方式分割成的小长方形零件最多有( )
