题目内容
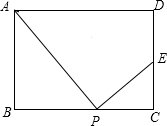 在矩形ABCD中,AB=2,AD=3,P是边BC上的任意一点(P与B、C不重合),作PE⊥AP,交CD于点E.
在矩形ABCD中,AB=2,AD=3,P是边BC上的任意一点(P与B、C不重合),作PE⊥AP,交CD于点E.
(1)判断△ABP与△PCE是否相似,并说明理由;
(2)连接BD,若PE∥BD,试求出此时BP的长.
解:(1)△ABP与△PCE相似.理由如下:
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAP+∠BPA=90°,
∵PE⊥AP,
∴∠CPE+∠BPA=90°,
∴∠BAP=∠CPE,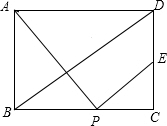
∴Rt△ABP∽Rt△PCE;
(2)由(1)得△ABP∽△PCE,
∴ =
= ,即
,即 =
= ,
,
∵PE∥BD,
∴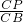 =
= ,即
,即 =
= ,
,
∴ =
= ,
,
∵AB=CD=2,BC=AD=3,
∴BP=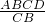 =
= .
.
分析:(1)△ABP与△PCE相似,根据矩形的性质和相似三角形的判定方法证明即可;
(2)由(1)可知△ABP与△PCE相似,所以 =
= ,即
,即 =
= ,又因为PE∥BD,
,又因为PE∥BD,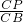 =
= ,即
,即 =
= ,所以
,所以 =
= ,利用已知数据即可求出BP的长.
,利用已知数据即可求出BP的长.
点评:本题综合考查了矩形的性质、相似三角形的判定和性质以及比例式的性质,题目难度中等.
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAP+∠BPA=90°,
∵PE⊥AP,
∴∠CPE+∠BPA=90°,
∴∠BAP=∠CPE,

∴Rt△ABP∽Rt△PCE;
(2)由(1)得△ABP∽△PCE,
∴
 =
= ,即
,即 =
= ,
,∵PE∥BD,
∴
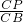 =
= ,即
,即 =
= ,
,∴
 =
= ,
,∵AB=CD=2,BC=AD=3,
∴BP=
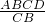 =
= .
.分析:(1)△ABP与△PCE相似,根据矩形的性质和相似三角形的判定方法证明即可;
(2)由(1)可知△ABP与△PCE相似,所以
 =
= ,即
,即 =
= ,又因为PE∥BD,
,又因为PE∥BD,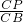 =
= ,即
,即 =
= ,所以
,所以 =
= ,利用已知数据即可求出BP的长.
,利用已知数据即可求出BP的长.点评:本题综合考查了矩形的性质、相似三角形的判定和性质以及比例式的性质,题目难度中等.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 7、如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( )
7、如图,在矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,AE=5,则AD等于( ) 如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系,并求自变量x的取值范围.
如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系,并求自变量x的取值范围. 如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.求证:AE=BF.
如图,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.求证:AE=BF. 在矩形ABCD中,AB=8,AD=6,E为AB边上一点,连接DE,过C作CF垂直DE.
在矩形ABCD中,AB=8,AD=6,E为AB边上一点,连接DE,过C作CF垂直DE. 如图,在矩形ABCD中,AF、BE、CE、DF分别是矩形的四个角的角平分线,E、M、F、N是其交点,求证:四边形EMFN是正方形.
如图,在矩形ABCD中,AF、BE、CE、DF分别是矩形的四个角的角平分线,E、M、F、N是其交点,求证:四边形EMFN是正方形.