题目内容
如图,点A(1,6)和点M(m,n)都在反比例函数y= (x>0)的图象上,
(x>0)的图象上,
(1)k的值为 ;
(2)当m=3,求直线AM的解析式;
(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.

解:(1)将A(1,6)代入反比例解析式得:k=6;
故答案为:6;
(2)将x=3代入反比例解析式y= 得:y=2,即M(3,2),
得:y=2,即M(3,2),
设直线AM解析式为y=ax+b,
把A与M代入得: ,
,
解得:a=﹣2,b=8,
∴直线AM解析式为y=﹣2x+8;
(3)直线BP与直线AM的位置关系为平行,理由为:
当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,
∵A(1,6),M(m,n),且mn=6,即n= ,
,
∴B(0,6),P(m,0),
∴k直线AM= =
= =
= =﹣
=﹣ =﹣
=﹣ ,k直线BP=
,k直线BP= =﹣
=﹣ ,即k直线AM=k直线BP,
,即k直线AM=k直线BP,
则BP∥AM.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





 、
、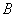 、
、 三艘船正在捕鱼作业,
三艘船正在捕鱼作业, 的度数;
的度数; ,
, )
) 

 =0.56,
=0.56, =0.60,
=0.60,  =0.50,
=0.50,  =0.45,则成绩最稳定的是( )
=0.45,则成绩最稳定的是( ) =30°,则∠
=30°,则∠ 的值为 .
的值为 . 表示不大于
表示不大于 的最大整数,例如:
的最大整数,例如:  ,
, ,
, ;用
;用 表示大于
表示大于 ,
, ,
, .解决下列问题:
.解决下列问题: = ,
= ,  = .
= . =2,则
=2,则 的取值范围是 ;若
的取值范围是 ;若 =-1,则
=-1,则 的取值范围是 .
的取值范围是 . ,求
,求