Question

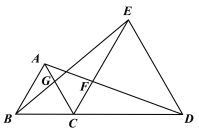
【题目】如图，点C为线段BD上一点，△ABC、△CDE都是等边三角形．AD与CE交于点F，BE与AC相交于点G．

（1）求证：△ACD≌△BCE；

（2）若CF+CG=8，BD=18，求△ACD的面积．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）证明∠BCE=∠DCA，再利用全等三角形判定定理（SAS）证明△ACD≌△BCE；

（2）过G,F作BD垂线段，分别交BD的垂线段GM,FN，证明△BCG≌△ACF，得出CG=CF=4，得出GM和FN的值，再代入面积公式求出△ACD的面积

（1）∵△ABC，△CDE是等边三角形，∴AC=BC,CD=CE,∠ACB=∠DCE=60°

∴∠ACB+∠ACE=∠DCE+∠ACE，即∠BCE=∠DCA

∴△ACD≌△BCE

（2）由（1）得△ACD≌△BCE，∴∠CBG=∠CAF

又∵∠ACF=∠BCG=60°，BC=AC，∴△BCG≌△ACF

∴，CG=CF，而CF+CG=8，∴CG=CF=4

过G,F作BD垂线段，分别交BD的垂线段GM,FN

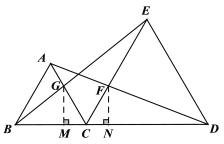
又∵∠ACB=∠DCE=60°

∴GM=CG=2

FN=CF=2

∴

=

=

=

=

=