题目内容
若|3-x|-|x+2|的最小值为a，最大值为b，则ab= ．
考点：绝对值
专题：综合题
分析：把x的取值分为x≥3，-2＜x＜3，x≤-2，然后看其最大值和最小值，最后确定a，b的值．
解答：解：当x≥3，|3-x|-|x+2|=x-3-x-2=-5，
当-2＜x＜3，|3-x|-|x+2|=3-x-x-2=1-2x，
当x≤-2，|3-x|-|x+2|=3-x+x+2=5，
∴-5≤|3-x|-|x+2|≤5，
则a=-5，b=5，
∴ab=-25．
故答案为-25．
当-2＜x＜3，|3-x|-|x+2|=3-x-x-2=1-2x，
当x≤-2，|3-x|-|x+2|=3-x+x+2=5，
∴-5≤|3-x|-|x+2|≤5，
则a=-5，b=5，
∴ab=-25．
故答案为-25．
点评：此题主要考查了绝对值的性质，能够根据已知条件正确地判断出a、b的值是解答此题的关键．
练习册系列答案
相关题目
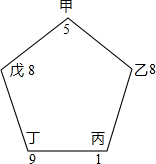甲、乙、丙、丁、戊五名同学手拉手围成一个五边形，每个人心中想一个数，相邻的两个人把所想两数的平均数告诉与他们不相邻的那个人，结果如图所示，则乙心中所想的数是
少30°，请你计算出这个角的大小． 
y－1是（ ）．
= .