题目内容
16. 如图,在Rt△ABC中,∠C=90°,CA=CB=2,分别以A,B,C为圆心,以1为半径画弧,三条弧与AB所围成的阴影部分的面积是2-$\frac{π}{2}$.
如图,在Rt△ABC中,∠C=90°,CA=CB=2,分别以A,B,C为圆心,以1为半径画弧,三条弧与AB所围成的阴影部分的面积是2-$\frac{π}{2}$.
分析 根据等腰直角三角形的性质得到∠A=∠B=45°,根据扇形的面积的面积公式求得三个扇形的面积,于是得到阴影部分的面积=△ABC的面积-三个扇形的面积.
解答 解:∵∠C=90°,CA=CB=2,
∴∠A=∠B=45°,
∴三条弧所组成的三个扇形的面积为$\frac{90π×{1}^{2}}{360}$+$\frac{45π×{1}^{2}}{360}$+$\frac{45π×{1}^{2}}{360}$=$\frac{π}{2}$,
△ABC的面积为$\frac{1}{2}×2×2=2$,
∴阴影部分的面积=2-$\frac{π}{2}$,
故答案为:2-$\frac{π}{2}$.
点评 本题考查了扇形的面积,等腰直角三角形的性质,熟记扇形的面积公式是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 已知:如图,B,C两点把线段AD分成2:3:4三部分,M是线段AD的中点,CD=16cm,求:
已知:如图,B,C两点把线段AD分成2:3:4三部分,M是线段AD的中点,CD=16cm,求: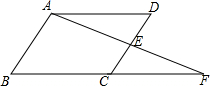 如图,在?ABCD中,CE=$\frac{1}{2}$ED,AE,BC的延长线交于点F.若△ECF的面积为1.求四边形ABCE的面积.
如图,在?ABCD中,CE=$\frac{1}{2}$ED,AE,BC的延长线交于点F.若△ECF的面积为1.求四边形ABCE的面积. 已知直线a,b,点P是a,b外的任意一点,过点P分别画a,b的垂线.
已知直线a,b,点P是a,b外的任意一点,过点P分别画a,b的垂线.