题目内容
阅读理解题:
定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(2+i)+(3-4i)=(2+3)+(1-4)i=5-3i.
(1)填空:i3= ,i4= .
(2)计算:①(1+i)(1-i); ②(1+i)2;
(3)试一试:请利用以前学习的有关知识将
化简成a+bi的形式.
定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(2+i)+(3-4i)=(2+3)+(1-4)i=5-3i.
(1)填空:i3=
(2)计算:①(1+i)(1-i); ②(1+i)2;
(3)试一试:请利用以前学习的有关知识将
| 2+i |
| 2-i |
考点:整式的混合运算,实数的运算,分式的混合运算
专题:阅读型,新定义
分析:(1)根据已知i2=-1代入求出即可;
(2)①先根据平方差公式进行计算,再代入求出即可;
②先根据完全平方公式展开,再代入求出即可;
(3)先根据平方差公式分母有理化,再根据公式进行计算,最后代入求出即可.
(2)①先根据平方差公式进行计算,再代入求出即可;
②先根据完全平方公式展开,再代入求出即可;
(3)先根据平方差公式分母有理化,再根据公式进行计算,最后代入求出即可.
解答:解:(1)i3=i2×i=-i;
i4=(-1)2=1,
故答案为:-i,1.
(2)①(1+i)(1-i)
=1-i2
=1-(-1)
=2;
②(1+i)2
=1+2i+i2
=2i;
(3)原式=
=
=
=
+
i.
i4=(-1)2=1,
故答案为:-i,1.
(2)①(1+i)(1-i)
=1-i2
=1-(-1)
=2;
②(1+i)2
=1+2i+i2
=2i;
(3)原式=
| (2+i)2 |
| (2-i)(2+i) |
=
| 4+4i+i2 |
| 4-i2 |
=
| 4+4i-1 |
| 4-(-1) |
=
| 3 |
| 5 |
| 4 |
| 5 |
点评:本题考查了平方差公式,完全平方公式,分母有理化的应用,主要考查学生的理解能力和计算能力,题目比较好,难度适中.

练习册系列答案
相关题目
方程组
的解与x与y的值相等,则k等于( )
|
| A、1 | B、-1 | C、2 | D、-2 |
一条直线y=kx+b其中k+b=-6,kb=8,那么该直线经过( )
| A、第二、四象限 |
| B、第一、二、三象限 |
| C、第一、三象限 |
| D、第二、三、四象限 |
已知?ABCD中,∠A+∠C=80°,则∠B的度数为( )
| A、80° | B、100° |
| C、120° | D、140° |
 如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.请完整说明为何△ABC与△DEC全等的理由.
如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.请完整说明为何△ABC与△DEC全等的理由.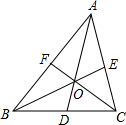 如图,△ABC的周长为18cm,BE、CF分别为AC、AB边上的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,求BD的长.
如图,△ABC的周长为18cm,BE、CF分别为AC、AB边上的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,求BD的长.