题目内容
15．
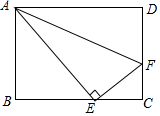如图，沿AE折叠长方形一边AD，点D落在BC边的点F处，已知BC=10cm，AB=8cm，求FC的长．
分析 由图形翻折变换的性质可知，AD=AE，DF=EF，根据勾股定理得出BE=6cm，设DF=xcm，则FC=（8-x）cm，在Rt△CEF中利用勾股定理即可求解．
解答 解：∵△AEF是△AED沿直线AE折叠而成，AB=8cm，BC=10cm，
∴AD=AF=10cm，EF=DF，设DF=x，则FC=8-x，
在Rt△ABE中，AE2=AB2+BE2，即102=82+BE2，
解得BE=6，
∴EC=BC-BE=10-6=4cm．
在Rt△CFE中，FE2=CE2+CF2，即x2=（8-x）2+42，
∴x=5，
∴FC=8-5=3cm，
∴FC的长为3cm．
点评 本题考查的是图形翻折变换的性质，即折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
练习册系列答案
相关题目
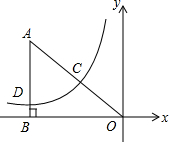如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直于x轴、垂足为点B，反比例函数y=$\frac{k}{x}$（x＜0）的图象经过AO的中点C、且与AB相交于点D，OB=8、AD=6．
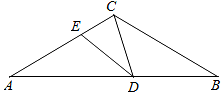如图，△ABC中，AC=BC，∠ACB=120°，点D在AB边上运动（D不与A、B重合），连结CD．作∠CDE=30°，DE交AC于点E．
已知线段a，b用尺规作一条线段c，使c=a+b．（不写作法，保留作图痕迹）
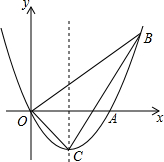如图，已知抛物线经过点A（2，0），B（3，3）及原点O，顶点为C．
若要使图中的展开图按虚线折叠成正方体后，相对面上两个数之和为10，则x+y=16．