题目内容
在⊙O中，弦AB=16cm，弦心距OC=6cm，那么该圆的半径为________cm．
10
分析：根据题意画出相应的图形，由OC垂直于AB，利用垂径定理得到C为AB别的中点，由AB的长求出BC的长，再由弦心距OC的长，利用勾股定理求出OB的长，即为圆的半径．
解答：
解：∵AB=16cm，OC⊥AB，
∴BC=AC=
AB=8cm，
又OC=6cm，
在Rt△BOC中，利用勾股定理得：OB=
=10cm．
故答案为：10
点评：此题考查了勾股定理，以及垂径定理，熟练掌握定理是解本题的关键．
分析：根据题意画出相应的图形，由OC垂直于AB，利用垂径定理得到C为AB别的中点，由AB的长求出BC的长，再由弦心距OC的长，利用勾股定理求出OB的长，即为圆的半径．
解答：
解：∵AB=16cm，OC⊥AB，∴BC=AC=
AB=8cm，又OC=6cm，
在Rt△BOC中，利用勾股定理得：OB=
=10cm．故答案为：10
点评：此题考查了勾股定理，以及垂径定理，熟练掌握定理是解本题的关键．
练习册系列答案
相关题目
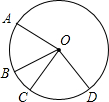如图，在⊙O中，弦AB=CD，图中的线段、角、弧分别具有相等关系的量共有（不包括AB=CD）（ ）| A、10组 | B、7组 | C、6组 | D、5组 |
如图，在⊙O中，弦AB⊥弦CD于E，弦AG⊥弦BC于F点，连EF，CD与AG相交于M点，则下列结论：①BD=BG；②DE=EM；③∠ACD=∠AFE；④AF=BF，其中正确的有
如图，在⊙O中，弦AB与弦CD相交于点E，且AB=CD．
如图，在⊙O中，弦AB=3.6cm，圆周角∠ACB=30°，则⊙O的直径等于（ ）