题目内容
如图，在⊙O中，弦AB与弦CD相交于点E，且AB=CD．求证：BE=DE．
分析：先连接BC、AD，由AB=CD可知
=
，故可得出
=
，故可得出BC=AD，由全等三角形的判定定理可得出△BEC≌△DEA，根据三角形的对应边相等即可得出结论．
 |
| AB |
|
| CD |
|
| BC |
|
| AD |
解答：
证明：先连接BC、AD，
∵AB=CD，
∴
=
，
∵
=
，
∴BC=AD，
在△BEC与△DEA中，
∵
，
∴△BEC≌△DEA（ASA），
∴BE=DE．
证明：先连接BC、AD，∵AB=CD，
∴
|
| AB |
|
| CD |
∵
|
| BC |
|
| AD |
∴BC=AD，
在△BEC与△DEA中，
∵
|
∴△BEC≌△DEA（ASA），
∴BE=DE．
点评：本题考查的是圆心角、弧、弦的关系及全等三角形的判定与性质，根据题意构造出全等三角形是解答此题的关键．
练习册系列答案
相关题目
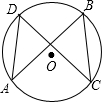已知：如图，在⊙O中，弦AD=BC．求证：AB=CD．
4、如图，在⊙O中，弦BC∥半径OA，AC与OB相交于M，∠C=20°，则∠AMB的度数为（ ）
标系．
如图，在⊙O中，弦AB=BC=CD，且∠ABC=140°，则∠AED=（ ）
如图，在⊙O中，弦AB与CD相交于点P，连接AC、DB．