题目内容
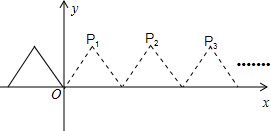 如图所示,将边长为2的等边三角形沿x轴正方向连续翻折2013次,依次得到点P1,P2,P3…P2013.则点P2013的坐标是________.
如图所示,将边长为2的等边三角形沿x轴正方向连续翻折2013次,依次得到点P1,P2,P3…P2013.则点P2013的坐标是________.
(4025, )
)
分析:根据等边三角形的性质易求得P1的坐标为(1, ),在等边三角形翻折的过程中,P点的纵坐标不变,而每翻折一次,横坐标增加2个单位(即等边三角形的边长),可根据这个规律求出点P2013的坐标.
),在等边三角形翻折的过程中,P点的纵坐标不变,而每翻折一次,横坐标增加2个单位(即等边三角形的边长),可根据这个规律求出点P2013的坐标.
解答:∵边长为2的等边三角形,
∴P1(1, ),
),
而P1P2=P2P3=2,
∴P2(3, ),P3(5,
),P3(5, );
);
依此类推,Pn(1+2n-2, ),即Pn(2n-1,
),即Pn(2n-1, );
);
当n=2011时,P2013(4025, ).
).
故答案为:(4025, ).
).
点评:本题主要考查了规律型问题,通常要根据简单的条件得到一般化规律,然后根据规律求特定的值,难度适中.
 )
)分析:根据等边三角形的性质易求得P1的坐标为(1,
 ),在等边三角形翻折的过程中,P点的纵坐标不变,而每翻折一次,横坐标增加2个单位(即等边三角形的边长),可根据这个规律求出点P2013的坐标.
),在等边三角形翻折的过程中,P点的纵坐标不变,而每翻折一次,横坐标增加2个单位(即等边三角形的边长),可根据这个规律求出点P2013的坐标.解答:∵边长为2的等边三角形,
∴P1(1,
 ),
),而P1P2=P2P3=2,
∴P2(3,
 ),P3(5,
),P3(5, );
);依此类推,Pn(1+2n-2,
 ),即Pn(2n-1,
),即Pn(2n-1, );
);当n=2011时,P2013(4025,
 ).
).故答案为:(4025,
 ).
).点评:本题主要考查了规律型问题,通常要根据简单的条件得到一般化规律,然后根据规律求特定的值,难度适中.

练习册系列答案
相关题目
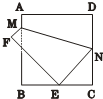 12、如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )
12、如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )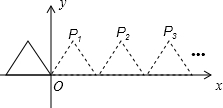
 如图所示,将边长为a的小正方形和边长为b的大正方形放在同一水平面上(b>a>0)
如图所示,将边长为a的小正方形和边长为b的大正方形放在同一水平面上(b>a>0) (2013•长宁区二模)如图所示,将边长为2的正方形纸片折叠,折痕为EF,顶点A恰好落在CD边上的中点P处,B点落在点Q处,PQ与CF交于点G.设C1为△PCG的周长,C2为△PDE的周长,则C1:C2=
(2013•长宁区二模)如图所示,将边长为2的正方形纸片折叠,折痕为EF,顶点A恰好落在CD边上的中点P处,B点落在点Q处,PQ与CF交于点G.设C1为△PCG的周长,C2为△PDE的周长,则C1:C2=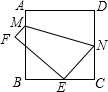 如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )
如图所示,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )