题目内容
 4、已知图形B是一个正方形,图形A由三个图形B构成,如图所示,请用图形A与B合拼成一个中心对称图形,但不是轴对称图形,并把它画在表格中.
4、已知图形B是一个正方形,图形A由三个图形B构成,如图所示,请用图形A与B合拼成一个中心对称图形,但不是轴对称图形,并把它画在表格中.分析:根据图形A与B合拼成一个中心对称图形,但不是轴对称图形,结合中心对称图形的性质得出旋转180°后与原图形完全重合得出符合要求的图案.
解答:解 :如图所示.
:如图所示.
 :如图所示.
:如图所示.点评:此题主要考查了中心对称图形与轴对称图形的性质,注意按要求得出A与B合拼成一个中心对称图形,但不是轴对称图形,这是易错点.

练习册系列答案
相关题目

 时,判断点P时否在直线ME上,并说明理由;
时,判断点P时否在直线ME上,并说明理由;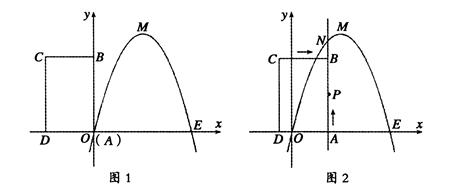
 时,判断点P时否在直线ME上,并说明理由;
时,判断点P时否在直线ME上,并说明理由;