题目内容
9. 已知:如图,AB=AC,点D、E分别在AB、AC上,且AD=AE,BE、CD交于点O,
已知:如图,AB=AC,点D、E分别在AB、AC上,且AD=AE,BE、CD交于点O,(1)求证:△ABE≌△ACD;
(2)求证:点O在线段BC的垂直平分线上.
分析 (1)利用SAS即可证明△ABE≌△ACD;
(2)由△ABE≌△ACD可得∠ABE=∠ACD,进而得到△BOC是等腰三角形,于是得到结论.
解答 解:(1)∵AE=AD,AC=AB,
∴DB=EC,
∵∠A是公共角,
∴△ABE≌△ACD(SAS);
(2)∵△ABE≌△ACD,
∴∠ABE=∠ACD,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠OBC=∠OCB,
∴△BOC是等腰三角形,
∴点O在线段BC的垂直平分线上.
点评 本题主要考查了全等三角形的判定与性质以及线段垂直平分线的知识,解题的关键是证明△ABE≌△ACD,此题难度不大.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目

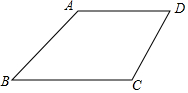 如图,在梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AD=$\frac{4}{3}\sqrt{6}$,BC=4$\sqrt{2}$,求CD的长.
如图,在梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AD=$\frac{4}{3}\sqrt{6}$,BC=4$\sqrt{2}$,求CD的长.