题目内容
1.已知直角三角形的两直角边长分别是9cm和5cm,斜边长是xcm.(1)估计x在哪两个整数之间;
(2)如果把x的结果精确到十分位,估计x的值在哪两个数之间,如果精确到百分位,用计算器验证你的估计值.
分析 利用勾股定理可得x的值,再利用“夹逼法”估算即可.
解答 解:(1)由勾股定理得:x=$\sqrt{{9}^{2}{+5}^{2}}$=$\sqrt{106}$
∵100<106<121,
∴10$<\sqrt{106}$<11,
∴x在10和11之间;
(2)∵10.22=104.04,10.32=106.09,
∴10.2<$\sqrt{106}$<10.3,
∴把x的结果精确到十分位,x的值在10.2和10.3两个数之间;
∵10.292=105.8841,10.302=106.09,
∴10.29<$\sqrt{106}$<10.30,
∴把x的结果精确到百分位,x的值在10.29和10.30两个数之间.
点评 本题主要考查了估算无理数的大小,利用“夹逼法”是解答此题的关键.

练习册系列答案
相关题目
 在梯形ABCD中,AH∥DC,E是AB的中点,直线ED分别与对角线AC和BC的延长线交于M,N点.求证:MD•NE=ND•ME.
在梯形ABCD中,AH∥DC,E是AB的中点,直线ED分别与对角线AC和BC的延长线交于M,N点.求证:MD•NE=ND•ME. 如图,在△ABC中,已知AD是∠BAC的角平分线,∠B=65°,∠C=54°
如图,在△ABC中,已知AD是∠BAC的角平分线,∠B=65°,∠C=54°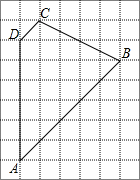 如图所示,图中小正方形的边长为1,试求图中梯形ABCD的面积,你有哪些方法?与同伴进行交流.
如图所示,图中小正方形的边长为1,试求图中梯形ABCD的面积,你有哪些方法?与同伴进行交流.