Question

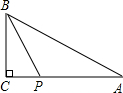如图，Rt△ABC中，∠C=90°，∠A=30°，P为AC边上一点，PC=2，∠PBC=30°．
（1）若PD⊥AB于D，在图中画出线段PD；
（2）点P到斜边AB的距离等于______．

Answer 1

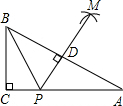解：（1）分别以点B为圆心、BP为半径，以点A为圆心、AP为半径在AB的另一侧画弧交于一点M，连接PM交AB于D，则PD⊥AB；

（2）∵Rt△ABC中，∠C=90°，∠A=30°，
∴∠ABC=60°，
又，∠PBC=30°，
∴∠PBD=∠PBC=30°，
由已知和作图得：∠C=PDB=90°，
BP=BP，
∴△PBC≌△PBD，
∴PD=PC=2，
即点P到斜边AB的距离等于 2．
故答案为：2．
分析：（1）分别以点B为圆心、BP为半径，以点A为圆心、AP为半径在AB的另一侧画弧交于一点M，连接PM交AB于D，则PD⊥AB；
（2）由已知Rt△ABC中，∠C=90°，∠A=30°，所以得∠ABC=60°，又由∠PBC=30°得∠PBD=30°，所以推出△PBC≌△PBD，得点P到斜边AB的距离PD=PC=2．
点评：此题考查的知识点是含30°的直角三角形，关键是正确作图通过证明△PBC≌△PBD求点P到斜边AB的距离．