题目内容
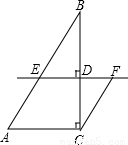
（2006•河南）如图所示，把腰长为1的等腰直角三角形折叠两次后，得到的一个小三角形的周长是 ．
【答案】分析：求出三个三角形的相似比，然后利用相似三角形的相似比就是周长比求第三个小三角形的周长．
解答：解：根据勾股定理可知腰长为1，则斜边为
，折叠后所得的三角形与原三角形相似，但斜边成了1，所以相似比是
，同理第三个小三角形与第二个三角形的相似比也
，得到第三个三角形的斜边是
，所以第一个与第三个的相似比是
即2：1，第一个三角形的周长为2+
，所以第三个就是
，即1+
．
点评：此题主要考查相似三角形的性质及翻折变换的性质的综合运用．
解答：解：根据勾股定理可知腰长为1，则斜边为
，折叠后所得的三角形与原三角形相似，但斜边成了1，所以相似比是，同理第三个小三角形与第二个三角形的相似比也，得到第三个三角形的斜边是，所以第一个与第三个的相似比是即2：1，第一个三角形的周长为2+，所以第三个就是，即1+．点评：此题主要考查相似三角形的性质及翻折变换的性质的综合运用．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
（2006•河南）如图，∠AOB=45°，过OA上到点O的距离分别为1，2，3，4，5 …的点作OA的垂线与OB相交，再按一定规律标出一组如图所示的黑色梯形．设前n个黑色梯形的面积和为Sn．
（1）请完成上面的表格；
（2）已知Sn与n之间满足一个二次函数关系，试求出这个二次函数的解析式．
| n | 1 | 2 | 3 | … |
| Sn | … |
（2）已知Sn与n之间满足一个二次函数关系，试求出这个二次函数的解析式．
（2006•河南）如图，∠AOB=45°，过OA上到点O的距离分别为1，2，3，4，5 …的点作OA的垂线与OB相交，再按一定规律标出一组如图所示的黑色梯形．设前n个黑色梯形的面积和为Sn．
（1）请完成上面的表格；
（2）已知Sn与n之间满足一个二次函数关系，试求出这个二次函数的解析式．
| n | 1 | 2 | 3 | … |
| Sn | … |
（2）已知Sn与n之间满足一个二次函数关系，试求出这个二次函数的解析式．
x+4分别交x轴、y轴于A、B两点．
