Question

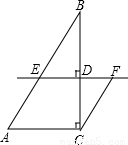
（2006•河南）如图△ABC中，∠ACB=90度，AC=2，BC=3．D是BC边上一点，直线DE⊥BC于D，交AB于点E，CF∥AB交直线DE于F．设CD=x．
（1）当x取何值时，四边形EACF是菱形？请说明理由；
（2）当x取何值时，四边形EACD的面积等于2？

Answer 1

【答案】分析：（1）ED、AC同时垂直于BC，因此EF∥AC，又有CF∥AB，那么四边形ACFE是个平行四边形，要想使其为菱形，就必须让CF=AC=2，然后用x表示出，CF、DF的值．在Rt△CDF中用勾股定理求出x的值即可．
（2）由于四边形ACDE是个直角梯形，可根据其面积公式求出关于x的一元二次方程，然后求出x的值．
解答：解：（1）∵在△ABC中，∠ACB=90°，
∴AC⊥BC，
又∵DE⊥BC，
∴EF∥AC
又∵AE∥CF，
∴四边形EACF是平行四边形．
当CF=AC时，四边形ACFE是菱形．
此时，CF=AC=2，BD=3-x，tanB=，
∵tanB=．
∴ED=BD•tanB=（3-x）．
∴DF=EF-ED=2-（3-x）=x．
在Rt△CDF中，由勾股定理得CD²+DF²=CF²，
∴x²+（x）²=2²，
∴x=±（负值不合题意，舍去）．
即当x=时，四边形ACFE是菱形．

（2）由已知得，四边形EACD是直角梯形，S_梯形EACD=DC•（DE+AC）=×（4-x）•x=-x²+2x，
依题意，得-x²+2x=2．
整理，得x²-6x+6=0．
解之，得x₁=3-，x₂=3+．
∵x=3+＞BC=3，
∴x=3+舍去．
∴当x=3-时，梯形EACD的面积等于2．
点评：本题的关键是如何判定四边形EFCA是菱形，菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：①定义，②四边相等，③对角线互相垂直平分．