题目内容
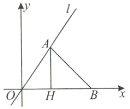
【题目】直线AB:![]() 分别于x,y轴交于A,B两点,过点B的直线交x轴正半轴于点C,且OB:OC=3:1.
分别于x,y轴交于A,B两点,过点B的直线交x轴正半轴于点C,且OB:OC=3:1.
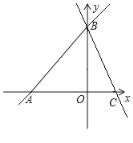
(1)直接写出点A、B、C的坐标;
(2)在线段OB上存在点P,使点P到B,C的距离相等,求出点P的坐标;
(3)在x轴上方存在点D,使得以点A,B,D为顶点的三角形与△ABC全等,求出点D的坐标.
【答案】(1)A(![]() ,0)、B(0,3)、C(1,0);(2)P(0,
,0)、B(0,3)、C(1,0);(2)P(0,![]() );(3)(-4,3)或(-3,4)
);(3)(-4,3)或(-3,4)
【解析】
(1)分别令y=0,x=0求得点A、B的坐标,OB的长度,结合OB:OC=3:1可求出点C的坐标;
(2)设OP=x,则PB=PC=3-x,在Rt△POC中,利用勾股定理可得出关于x的一元一次方程,解方程即可;
(3)画出图形,分△BAD≌△ABC和△ABD≌△ABC两种情况考虑:①当△BAD≌△ABC时,由OA=OB可得出∠BAC=45°,由全等三角形的性质可得出∠ABD=∠BAC=45°、BD=AC=4,利用内错角相等两直线平行可得出BD∥AC,结合BD的长度即可得出点D的坐标;②当△ABD≌△ABC时,有∠BAD=∠BAC=45°、AD=AC=4,由∠DAC=∠BAD+∠BAC可得出∠DAC=90°,结合BD的长度可得出点D的坐标;
(1)当y=0时,则x+3=0,x=-3,即点A(-3,0);
当x=0时,则y=3,即点B(0,3);
所以OB=3,
又∵OB:OC=3:1,
∴OC=1,
又∵过点B的直线交x轴正半轴于点C,
∴点C(1,0),
(2)如图所示:
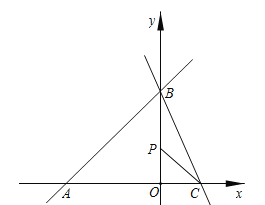
设OP=x,则PB=PC=3-x.
在Rt△POC中,∠POC=90°,
∴OP2+OC2=PC2,即x2+12=(3-x)2,
解得x=![]() ,
,
∴点P(0,![]() ),
),
(3)如图所示:分△BAD≌△ABC和△ABD≌△ABC两种情况考虑
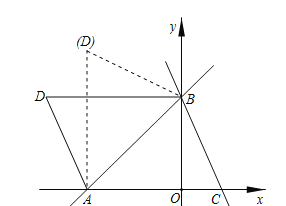
①当△BAD≌△ABC时,
∵OA=OB=3,
∴∠BAC=45°.
∵△BAD≌△ABC,
∴∠ABD=∠BAC=45°,BD=AC=4,
∴BD∥AC,
∴点D的坐标为(-4,3);
②当△ABD≌△ABC时,∠BAD=∠BAC=45°,AD=AC=4,
∴∠DAC=90°,
∴点D的坐标为(-3,4).
综上所述,点D的坐标为(-4,3)或(-3,4).