题目内容
 如图,将矩形OABC放置在平面直角坐标系xOy中,点A、C分别在x轴、y轴上,点B的坐标为(2,1),将矩形OABC绕着A点顺时针旋转90°得到矩形FADE.双曲线y=
如图,将矩形OABC放置在平面直角坐标系xOy中,点A、C分别在x轴、y轴上,点B的坐标为(2,1),将矩形OABC绕着A点顺时针旋转90°得到矩形FADE.双曲线y=| k |
| x |
(1)求k的值和直线MF的解析式;
(2)若直线MF交y轴于点N,连接BM,BN,求△BMN的面积.
考点:反比例函数综合题
专题:计算题
分析:(1)根据反比例函数图象上点的坐标特征得到k=2,则反比例函数解析式为y=
,再根据旋转的性质得到FA=OA=2,AD=AB=1,则F点坐标为(2,2),D点坐标为(3,0),然后利用反比例函数图象上点的坐标特征得到M点的坐标为(3,
),再利用待定系数法求直线MF的解析式;
(2)利用三角形面积公式和S△BMN=S△BFN+S△BFM进行计算.
| 2 |
| x |
| 2 |
| 3 |
(2)利用三角形面积公式和S△BMN=S△BFN+S△BFM进行计算.
解答:解:(1)把B(2,1)代入y=
得k=2×1=2,
∴反比例函数解析式为y=
,
∵矩形OABC绕着A点顺时针旋转90°得到矩形FADE,
∴FA=OA=2,AD=AB=1,
∴F点坐标为(2,2),D点坐标为(3,0),
把x=3代入y=
得y=
,
∴M点的坐标为(3,
)
设直线MF的解析式为y=ax+b,
把F(2,2),M(3,
)代入得
,解得
,
∴直线MF的解析式为y=-
x+
;
(2)S△BMN=S△BFN+S△BFM
=
×(2-1)×2+
×(2-1)×1
=
.
| k |
| x |
∴反比例函数解析式为y=
| 2 |
| x |
∵矩形OABC绕着A点顺时针旋转90°得到矩形FADE,
∴FA=OA=2,AD=AB=1,
∴F点坐标为(2,2),D点坐标为(3,0),
把x=3代入y=
| 2 |
| x |
| 2 |
| 3 |
∴M点的坐标为(3,
| 2 |
| 3 |
设直线MF的解析式为y=ax+b,
把F(2,2),M(3,
| 2 |
| 3 |
|
|
∴直线MF的解析式为y=-
| 4 |
| 3 |
| 14 |
| 3 |
(2)S△BMN=S△BFN+S△BFM
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 2 |
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和旋转的性质;会运用待定系数法求一次函数解析式;理解图形与坐标的关系.

练习册系列答案
相关题目
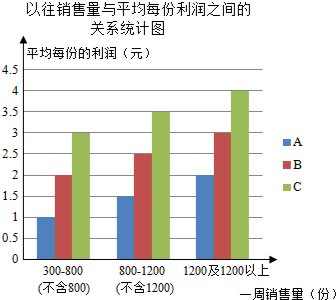 配餐公司为某学校提供A、B、C三类午餐供师生选择,三类午餐每份的价格分别是:A餐6元,B餐8元,C餐10元,为做好下阶段的营销工作,配餐公司根据该校上周A、B、C三类午餐购买情况,将所得的数据处理后,制成统计表:根据以往销售量与平均每份利润之间的关系,制成统计图(如图)
配餐公司为某学校提供A、B、C三类午餐供师生选择,三类午餐每份的价格分别是:A餐6元,B餐8元,C餐10元,为做好下阶段的营销工作,配餐公司根据该校上周A、B、C三类午餐购买情况,将所得的数据处理后,制成统计表:根据以往销售量与平均每份利润之间的关系,制成统计图(如图)
 如图,A、B、C、D依次为一直线上4个点,BC=2,△BCE为等边三角形,⊙O过A、D、E3点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系式为
如图,A、B、C、D依次为一直线上4个点,BC=2,△BCE为等边三角形,⊙O过A、D、E3点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系式为