题目内容
把直线
图象向________单位长度可得到
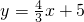的图象．
上平移5个
分析：直接根据“上加下减”的原则进行解答即可．
解答：由“上加下减”的原则可知，把直线y=
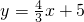x的图象向上平移5个单位即可得到的图象．
故答案为：上平移5个．
点评：本题考查的是一次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．
分析：直接根据“上加下减”的原则进行解答即可．
解答：由“上加下减”的原则可知，把直线y=
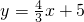x的图象向上平移5个单位即可得到的图象．故答案为：上平移5个．
点评：本题考查的是一次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．
练习册系列答案
相关题目
在平面直角坐标系中，点P从原点O出发，每次向上平移2个单位长度或向右平移1个单位长度．
（1）实验操作：
在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点
的坐标填写在表格中：
（2）观察发现：
任一次平移，点P可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数 的图象上；平移2次后在函数 的图象上…由此我们知道，平移n次后在函数 的图象上．（请填写相应的解析式）
（3）探索运用：
点P从点O出发经过n次平移后，到达直线y=x上的点Q，且平移的路径长不小于50，不超过56，求点Q的坐标．
（1）实验操作：
在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点
的坐标填写在表格中：| P从点O出发平移次数 | 可能到达的点的坐标 |
| 1次 | （0，2），（1，0） |
| 2次 | |
| 3次 |
任一次平移，点P可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数
（3）探索运用：
点P从点O出发经过n次平移后，到达直线y=x上的点Q，且平移的路径长不小于50，不超过56，求点Q的坐标．
（2012•泉州）如图，在方格纸中（小正方形的边长为1），反比例函数y=在平面直角坐标系中，点P从原点O出发，每次向上平移2个单位长度或向右平移1个单位长度．
（1）实验操作：
在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点
的坐标填写在表格中：
| P从点O出发平移次数 | 可能到达的点的坐标 |
| 1次 | （0，2），（1，0） |
| 2次 | |
| 3次 |
（2）观察发现：
任一次平移，点P可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数______的图象上；平移2次后在函数______的图象上…由此我们知道，平移n次后在函数______的图象上．（请填写相应的解析式）
（3）探索运用：
点P从点O出发经过n次平移后，到达直线y=x上的点Q，且平移的路径长不小于50，不超过56，求点Q的坐标．
在平面直角坐标系中，点P从原点O出发，每次向上平移2个单位长度或向右平移1个单位长度．
（1）实验操作：
在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点的坐标填写在表格中：
（2）观察发现：
任一次平移，点P可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数______的图象上；平移2次后在函数______的图象上…由此我们知道，平移n次后在函数______的图象上．（请填写相应的解析式）
（3）探索运用：
点P从点O出发经过n次平移后，到达直线y=x上的点Q，且平移的路径长不小于50，不超过56，求点Q的坐标．
（1）实验操作：
在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点的坐标填写在表格中：
| P从点O出发平移次数 | 可能到达的点的坐标 |
| 1次 | （0，2），（1，0） |
| 2次 | |
| 3次 |
任一次平移，点P可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数______的图象上；平移2次后在函数______的图象上…由此我们知道，平移n次后在函数______的图象上．（请填写相应的解析式）
（3）探索运用：
点P从点O出发经过n次平移后，到达直线y=x上的点Q，且平移的路径长不小于50，不超过56，求点Q的坐标．
次后在函数
的图象上．（请填写相应的解析式）
上的点Q，且平移的路径长不小于50，不超过56，求点Q的坐标．