题目内容
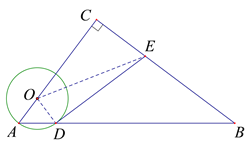
【题目】如图,在△ABC中,∠C=![]() ,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
(1)求证:∠EDB=∠B.
(2)若sinB=![]() ,AB=10,OA=2,求线段DE的长.
,AB=10,OA=2,求线段DE的长.

【答案】(1)见解析;(2)4.75
【解析】分析:(1)、连接OD,根据切线的性质得出∠ODA+∠EDB=![]() ,根据三角形内角和定理得出∠A+∠B=
,根据三角形内角和定理得出∠A+∠B=![]() ,根据OA=OD得出∠A=∠ODA,从而得出答案;(2)、连接OE,根据三角函数得出AC的长度,根据勾股定理得出BC的值,设DE=x,则BE=DE=x,CE=8-x,根据
,根据OA=OD得出∠A=∠ODA,从而得出答案;(2)、连接OE,根据三角函数得出AC的长度,根据勾股定理得出BC的值,设DE=x,则BE=DE=x,CE=8-x,根据![]() 得出答案.
得出答案.
详解:(1)解:连结OD,
∵DE与⊙O相切于点D,∴OD⊥DE. ∴∠ODE=![]() . ∴∠ODA+∠EDB=
. ∴∠ODA+∠EDB=![]() .
.
∵∠C=![]() , ∴∠A+∠B=
, ∴∠A+∠B=![]() . ∵OA=OD, ∴∠A=∠ODA. ∴∠EDB=∠B.
. ∵OA=OD, ∴∠A=∠ODA. ∴∠EDB=∠B.
(2)连结OE, ∵∠EDB=∠B, ∴EB=ED. ∵AB=10,sinB=![]() =
=![]() , ∴AC=6.
, ∴AC=6.
由勾股定理,得BC=8. 设DE=x,则EB=ED=x,CE=8-x.
∵∠C=∠ODE =![]() , ∴
, ∴![]() .
.
∴![]() , ∴
, ∴![]() , 即DE=
, 即DE=![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目