题目内容
△ABC中,∠A=35°,BD是AC边上的高,且BD2=AD•CD,则∠BCA的度数为 .
【答案】分析:根据相似三角形的判定,由已知可判定△ADB∽△BDC,进而求出∠A=∠CBD,即可求∠BCA的度数.
解答:
 解:有两种可能:△ABC为锐角三角形或钝角三角形时,
解:有两种可能:△ABC为锐角三角形或钝角三角形时,
①当△ABC为锐角三角形时,
∵BD2=AD•CD,
∴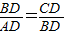 ,
,
∵BD是AC边上的高,
∴∠ADB=∠CDB=90°,
∴△ADB∽△BDC,
∴∠A=∠CBD,
∵∠A=35°,
∴∠CBD=35°,
∴∠BCA=∠BDC-∠CBD=90°-35°=55°.
②当△ABC为钝角三角形时,
∵BD2=AD•CD,
∴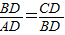 ,
,
∵BD是AC边上的高,
∴∠ADB=∠CDB=90°,
∴△ADB∽△BDC,
∴∠CBD=35°,
∴∠BCA=∠BDC+∠CBD=90°+35°=125°.
点评:本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边成比例、对应角相等.
解答:

 解:有两种可能:△ABC为锐角三角形或钝角三角形时,
解:有两种可能:△ABC为锐角三角形或钝角三角形时,①当△ABC为锐角三角形时,
∵BD2=AD•CD,
∴
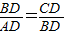 ,
,∵BD是AC边上的高,
∴∠ADB=∠CDB=90°,
∴△ADB∽△BDC,
∴∠A=∠CBD,
∵∠A=35°,
∴∠CBD=35°,
∴∠BCA=∠BDC-∠CBD=90°-35°=55°.
②当△ABC为钝角三角形时,
∵BD2=AD•CD,
∴
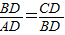 ,
,∵BD是AC边上的高,
∴∠ADB=∠CDB=90°,
∴△ADB∽△BDC,
∴∠CBD=35°,
∴∠BCA=∠BDC+∠CBD=90°+35°=125°.
点评:本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边成比例、对应角相等.

练习册系列答案
相关题目
 如图,在△ABC中,AC=2,AB=3,D是AC上一点,E是AB上一点,且∠ADE=∠B,设AD=x,AE=y,则y与x之间的函数关系式是( )
如图,在△ABC中,AC=2,AB=3,D是AC上一点,E是AB上一点,且∠ADE=∠B,设AD=x,AE=y,则y与x之间的函数关系式是( )A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
 如图,在△ABC中,AB=8,AC=6,BC=7,点D在AC上,AD=2,
如图,在△ABC中,AB=8,AC=6,BC=7,点D在AC上,AD=2,